Stereo Projections: Background, Mathematics, and Use

Stereo Perspective

Our final task is to extend the results of the previous pages to show how to generate separate perspective views of a scene to the left and right eyes. We will derive the expressions from scratch, and see that they lead to the presence of shears in the matrix: one for each eye.

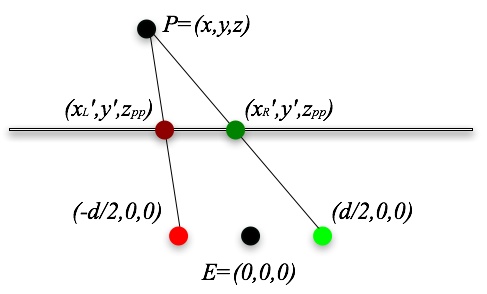
We wish to generate expressions for the point P as projected onto each of the left and right eyes. The eyes are separated only in the x direction of the eye coordinate system, hence y′ will be the same as we saw before. (Recall that we want to avoid vertical parallax in our stereo images.) Similarly, nothing need change in the z direction. We focus exclusively, then, on the projected x coordinates as seen by the left and right eye.

The left and right eyes are separated by a distance, d, as indicated in the figure. Following our logic from earlier in this section of the notes, it should be clear that:

z_pp/z = (x_L′ - (-d/2)) / (x - (-d/2)) and z_pp/z = (x_R′ - d/2) / (x - d/2)

Solving for x_L′ and x_R′ (and multiplying both sides by z to get the coordinates of the desired projectively equivalent point):

x_L′z = z_ppx - dz/2 + dz_pp/2 and x_R′z = z_ppx + dz/2 - dz_pp/2