Stereo Projections: Background, Mathematics, and Use

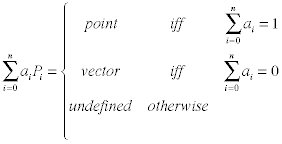
Allowed Mathematical Operations

Not all algebraic expressions involving points are well-defined. It is beyond the scope of these notes to completely explore this idea, however one important valid construction is the Barycentric combination of n affine points, R_i. Specifically, ∑a_iR_i is a Barycentric combination if and only if ∑a_i=1. Barycentric combinations always produce well-defined points.

Graphics systems commonly support a series of useful operations for geometry including rotations, scales, translations, shears, etc. Collectively, these transformations are called affine transformations or affine maps. Mathematically, we say they are a mapping of points in an affine space to other points in the same affine space. In these notes, we will use a functional notation – X(P) – to denote the application of an affine transformation, X, to some affine point, P.

Formally, then, an affine transformation is any mapping of affine points that preserves Barycentric combinations. That is, X is an affine transformation if and only if: for every point Q=∑a_iR_i, it is true that X(Q)=∑a_iX(R_i).

It can be shown that X is an n-dimensional affine transformation if and only if it can be written as: X(P) = MP + t where M is an nxn matrix and t is an n-dimensional vector.

Since we are interested in 3D geometry in these notes, let's specialize this result to that domain. An affine transformation such as a 3D rotation or scale can be written with a 3x3 matrix, M and a 3D vector, t. An arbitrary 3D point, P=(x,y,z) is then transformed as: X(P) = P′ = MP + t. Recalling our description of projective spaces, we can also write this as P^P′ = M_4x4P^P where P^P = (x,y,z,1) and M_4x4 is a 4x4 matrix in which the upper left 3x3 submatrix is M, the fourth column is (t_x, t_y, t_z, 1), and the fourth row is (0, 0, 0, 1).

Formally, we embed P in projective space and describe our affine transformation in that projective space. The fact that the bottom row is (0, 0, 0, 1) guarantees that transformed points are in the same affine space. That is, the fourth coordinate of P^P′ will always be 1.

The 4x4 matrix represents a single form that can be used to describe any affine transformation. Moreover, as we will see shortly, it can also be used to represent perspective transformations. The fact that this single form can be used for these two purposes explains why virtually all graphics APIs employ 4x4 matrices to represent all transformations. It also explains why graphics hardware includes support for 4x4 matrix multiplication.

Armed with this understanding, we can now return to our study of conventional perspective projections and their generalization to stereo perspective projections.