Stereo Projections: Background, Mathematics, and Use

Introduction

Linear planar geometric projections refer to mappings of 3D geometry onto an infinite plane (the projection plane) using a family of straight lines called projectors. There is an excellent survey by Carlbom and Paciorek that describes the history, mathematics, and common uses of planar geometric projections.

All families of projection lines used have the property that for every distinct point, P, (except for possibly one) in an affine space, there is a unique projection line, L, in the family that contains P. The linear planar projection of a point P is then defined as the intersection of L with the projection plane.

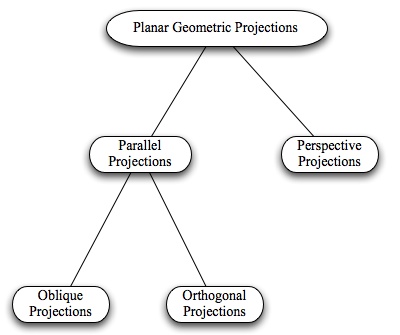
There are two major categories of planar projections. They are named according to how the corresponding projection line families are characterized. In the following, let us assume that a vector normal to the projection plane is n.

1. Parallel Projections: All projection lines are parallel to one another. We shall use d to denote the common projection line direction vector. Two common sub-categories are:
   1. Orthogonal Projections: All projection lines are perpendicular to the projection plane (i.e., d=sn for some non-zero real scalar, s).
   2. Oblique Projections: All projection lines strike the plane at some angle other than 90°, and d·n≠0.
   Mathematically, parallel projections can be viewed as a special case of perspective projections (described next) in which the eye moves to infinity. Our interest in these notes is in stereo projections, and they require that the eye be a finite distance from the scene, hence we will not consider parallel projections further in these notes. The interested reader is referred to section VII of a technical report on the Mathematics of Graphical Transformations.
2. Perspective Projections: All projection lines share a common point, namely the assumed position of the eye, E. For an arbitrary point P in an affine space, the projection line which contains it is simply the line determined by E and P. Therefore all such points, P (except E) lie on a unique perspective projection line. Furthermore, if that line is not parallel to the projection plane (i.e., if (P-E)·n≠0), then P has a unique finite projection which we shall call P′.