Linear Perspective
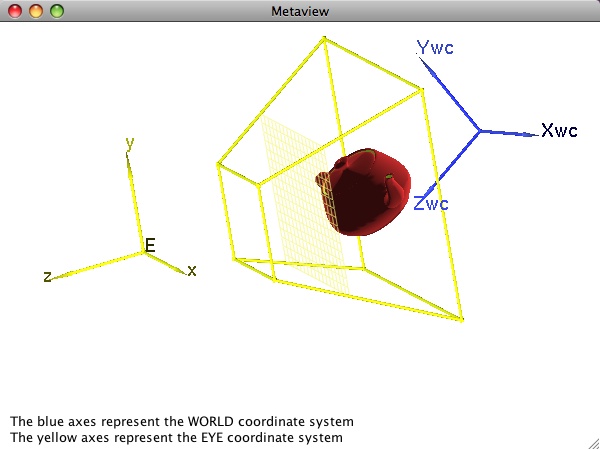
The Geometry of Perspective
It is common to study the geometry and detailed mathematics of projections using the eye coordinate system. Recall that this is a coordinate system in which the eye point E (i.e., the position of the viewer) is the origin, the x and y axes are parallel to the screen horizontal and vertical directions, respectively, and the z axis is determined from the right-hand rule. Hence the viewer's eye is at E, and s/he is looking down the negative z axis.
Geometry – initially defined in the world coordinate system – is first transformed into eye coordinates using an affine transformation as described in the previous section. After conversion to eye coordinates, the geometry is projected onto the projection plane via a parallel or perspective projection. Recall we shall only be interested here in perspective projections.
In the figure at the top of this page, the eye coordinate system is shown in yellow, and the world coordinate system is shown in blue. The Utah teapot represents a model being viewed. The projection plane is shown as a yellow gridded polygon in which the grid points symbolize pixels on the display. Note that the teapot model is entirely contained in the yellow perspective view frustum. Only geometry inside this frustum is mapped to the display. The front and rear of the frustum correspond to near and far clipping planes. The yellow color of the projection plane and view frustum emphasizes the fact that they are defined with respect to the eye coordinate system. The image below shows the actual image of the teapot on the display as determined by this viewing configuration.

EXERCISE
|
Run the metaview program and make sure you can reproduce the images on this page. Experiment with other view and projection settings as you familiarize yourself with the effect of the various viewing parameters. The major interactive controls are described in the html greeting page in the Control Panel window.
Unless otherwise stated later, we will implicitly assume throughout the remainder of these notes that geometry has been transformed into eye coordinates. The projection plane is always perpendicular to the eye coordinate system z axis and intersects it on the negative half of the axis. We will not always draw the various coordinate system axes in subsequent figures, but we will usually show and label the eye point E, the projection plane, and some geometry to be projected (sometimes just one or two points).

