Vector, Affine, and Projective Spaces
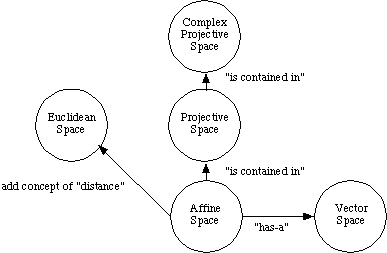
Spaces
Creating, rendering, editing, and all other manipulations we perform on graphical objects are implemented using mathematical operations on points and vectors. Everyone does it all the time. Nevertheless, it is important to have a deep understanding of our points and vectors (as well as the operations we are allowed to use on them) and how the affine and projective spaces in which they live relate. This understanding will help us not only to understand stereo projections, but also almost any geometric problem or analysis we encounter.
Our focus in this tutorial will be on Vector Spaces, Affine Spaces, and Projective Spaces. Other common spaces of interest are Euclidean and Complex Projective Spaces. The former adds the concepts of length and distance to an affine space; the latter allows coordinates to be complex numbers. We begin by examining the first three of these spaces.

