Vector, Affine, and Projective Spaces
Vector Spaces
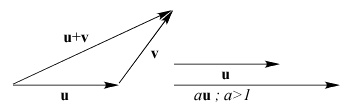
Definition: An n-dimensional vector space consists
of a set of vectors and two operations: addition
and scalar multiplication. The vector space is
closed under these two operations: addition of
two vectors yields a vector in the vector space;
multiplication of a vector by a scalar also produces
a vector in the vector space. Finally, there exists a
distinguished member of the set called the zero
vector 0 with the properties that
There are many sets that satisfy these properties. Polynomials of degree n, for example, form an n-dimensional vector space.
In these notes, we are of course only concerned with geometric objects, and it is clear that "geometric vectors" satisfy this definition. Specifically, we shall be interested in 3D vector spaces.

