Vector, Affine, and Projective Spaces
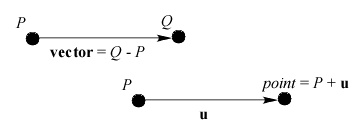
Affine Spaces
Definition: An n-dimensional affine space consists of a set of points, an associated n-dimensional vector space, and two operations: subtraction of two points in the set and addition of a point in the set and a vector in the associated vector space. The former produces a vector in the associated vector space, and the latter produces another point in the affine space.
Note: Unlike a vector space, which has the distinguished vector 0, an affine space does not include a distinguished point with special properties.

