Vector, Affine, and Projective Spaces
Projective Spaces and Projective Equivalence
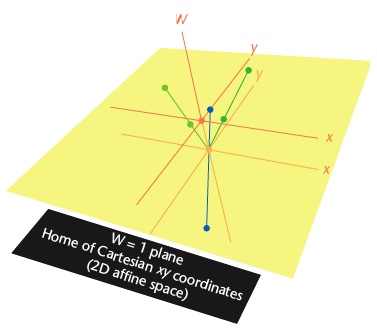
Definition: An (n + 1)-dimensional projective space is the space in which the points of an n-dimensional affine space are embedded. We denote the extra coordinate dimension as w and say that the affine points lie in the w = 1 plane of the projective space.
The figure on this page illustrates the n=2 case. The translucent yellow plane is the affine 2D plane. It is also the w=1 plane of a 3D projective space.
Definition: All projective space points on the line from the projective space origin through an affine point on the w = 1 plane are said to be projectively equivalent to the affine space point.
In the figure, all points on the light green line are projectively equivalent to the point symbolized by the green dot on the affine (w=1) plane. Similar remarks apply to the other projection lines in the figure.
It may not be clear right now what role projective spaces will play, but it turns out that the mathematics of perspective projections (and hence stereo perspective projections) are conveniently represented in projective space. That is, they can be represented using the same formalism as ordinary rotations, translations, and scales. This makes it much more convenient to integrate perspective transformations with these other transformations. The same cannot be said if we restrict ourselves to affine space and the operations defined for points and vectors in affine spaces.

