Stereo Projections: Background, Mathematics, and Use

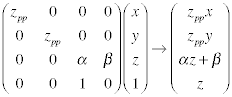
Matrix Representation

Visible surface determination (and other operations requiring depth information in images) are typically performed after the perspective projection. If we create the matrix exactly as shown on the previous page, we will lose our ability to perform these important tasks, because we lose all relative depth information. (Recall all points wind up with z = z_pp.)

We therefore need to do something a little more sophisticated with the third row of the matrix so that we can preserve relative depth. Rather than allowing all projected points to have z = z_pp, we will compute a z′ for each which preserves relative depth relationships among all the points in the scene.

So what should this third row look like? That is, on what should z′ depend? It should be clear that z′ cannot be a function of the x and y coordinates of a point. Two points with different x and y coordinates, but identical z coordinates before the transformation must be mapped to points that have the same z′ coordinate by the transformation. (You should take a moment and convince yourself that this is true.)

This means the first two elements of the third row must be zero, and hence the general form of the matrix will be as indicated above. Our challenge is to compute α and β so that relative depth is preserved. Recognizing that the perspective divide will result in the z coordinate of the affine point being z′ = α + β/z, we can determine appropriate values for α and β by applying the window-viewport limits in the z direction.

Different graphics APIs map the z direction differently. Some map z_min ≤ z_eye ≤ z_max to a normalized 0 ≤ z′ ≤ 1 range. This would give us two equations in two unknowns from which α and β are easily determined:

α + β/zmin = 0
α + β/zmax = 1

OpenGL uses an internal left-handed normalized range in which points on the near plane are mapped to -1, and points on the far plane are mapped to +1. This convention gives us the following two equations in our two unknowns:

α + β/(-n) = -1
α + β/(-f) = 1

('n' and 'f' stand for the distances to the 'near' and 'far' planes, respectively, as passed to the OpenGL routine glFrustum. They are negated above because we need to convert them from distances to actual eye z coordinates when writing the equations. That is, positive values for 'n' and 'f' correspond to distances along the line of sight, which is the negative z direction of the eye coordinate system.)

Solving for α and β, we get: α=(f+n)/(f-n) and β=2fn/(f-n).

Optional Appendix F of the OpenGL Programming Guide shows the perspective transformation matrix generated by a glFrustum call. Their matrix differs in two respects that are unimportant to us in these notes: They incorporate a window-viewport map in the x and y directions which we have not included because we don't need it here. Their matrix is essentially the negative of the matrix derived here. It is equivalent in that the same final affine point appears after the perspective divide. (You should convince yourself that this is true. That is, verify that the same affine point will appear following the perspective divide, whether you use the matrix as shown above or the negative of this matrix.) The difference is that their matrix will always generate positive w coordinates for visible points whereas the matrix as we derived it here will produce negative w coordinates for visible points. If you wish to create stereo perspective projection matrices for use in OpenGL programs, you must use their convention of always generating positive w coordinates for visible points. All geometry with negative w coordinates are clipped by the OpenGL engine before the perspective divide is performed. A convention such as this is necessary because after you apply the perspective divide, it is not possible to distinguish points in front of the eye from those behind it. We developed our matrix as shown here because the derivation seemed somewhat simpler (no need to introduce window-viewport maps) and slightly more intuitive (avoiding the need to introduce minus signs). Section VII of the technical report on graphical transformations includes the complete derivation of the OpenGL matrix shown in Appendix F of the OpenGL Programming Guide. If you wish to generate actual stereo projection matrices for use in OpenGL programs, you can either negate every element of the matrices shown here and then add window-viewport mapping accommodations in the x and y directions, or adapt the derivations given in the technical report (which include relevant window-viewport mappings) using the added stereo separation concepts described here.