-
[4] T. Panitanarak and S.M. Shontz,
A parallel log barrier-based mesh warping
algorithm for distributed memory machines, Engineering with Computers, 34(1):59-76, 2018.
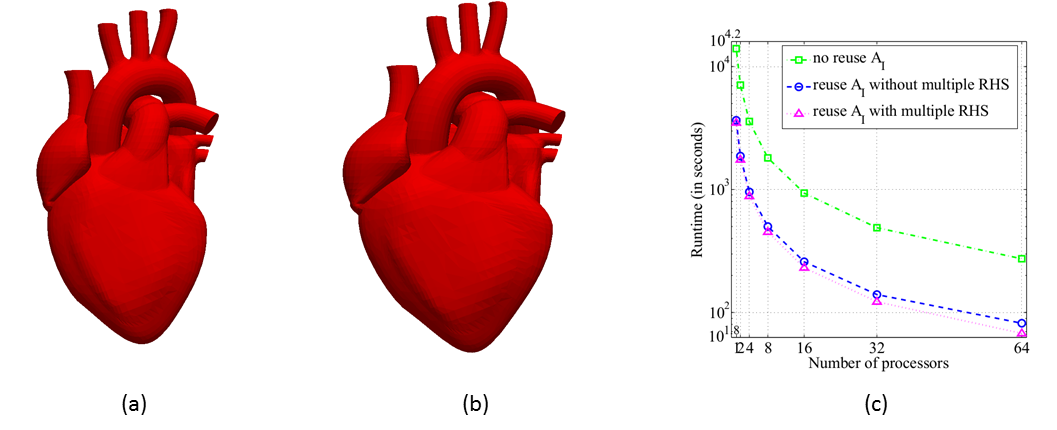
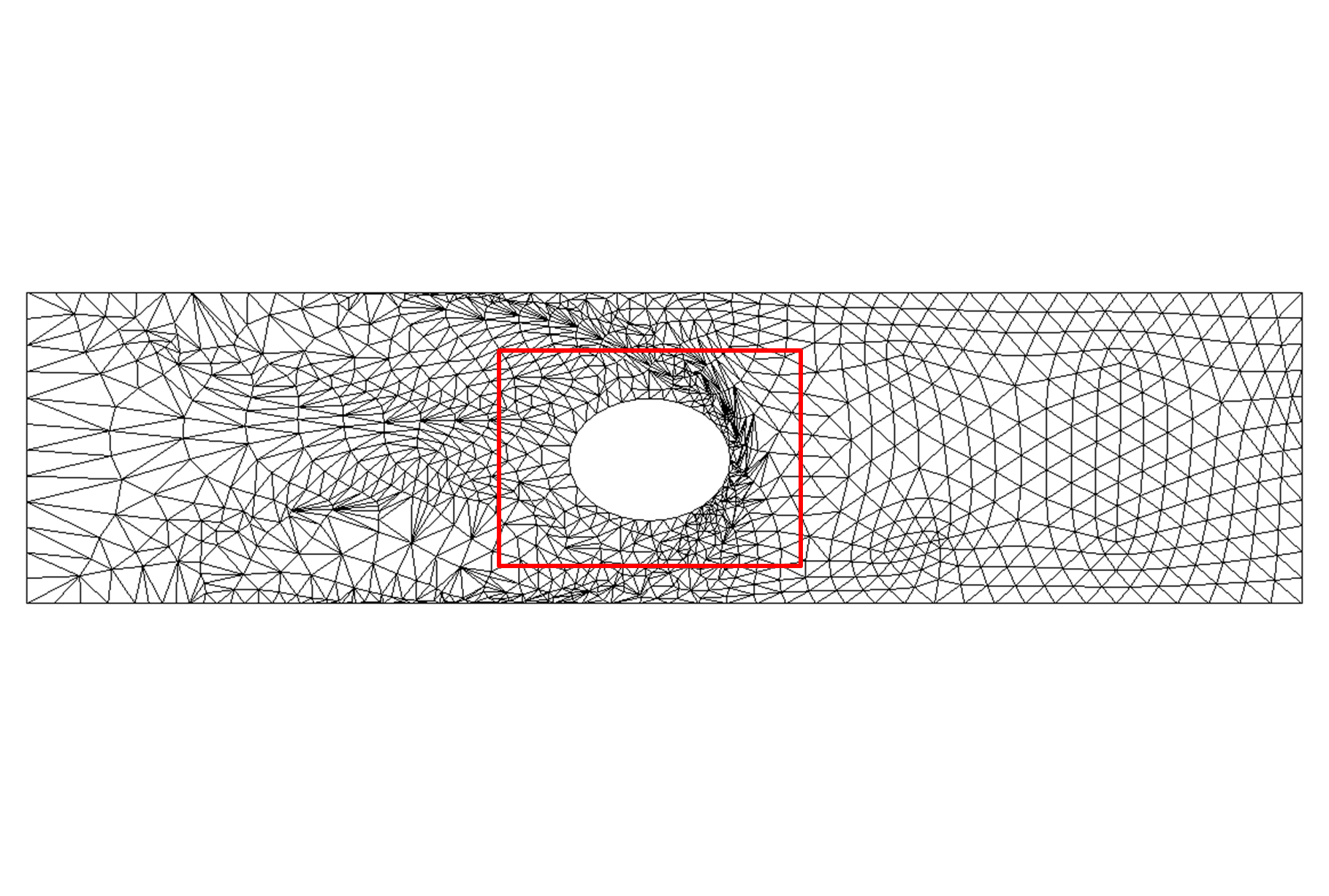
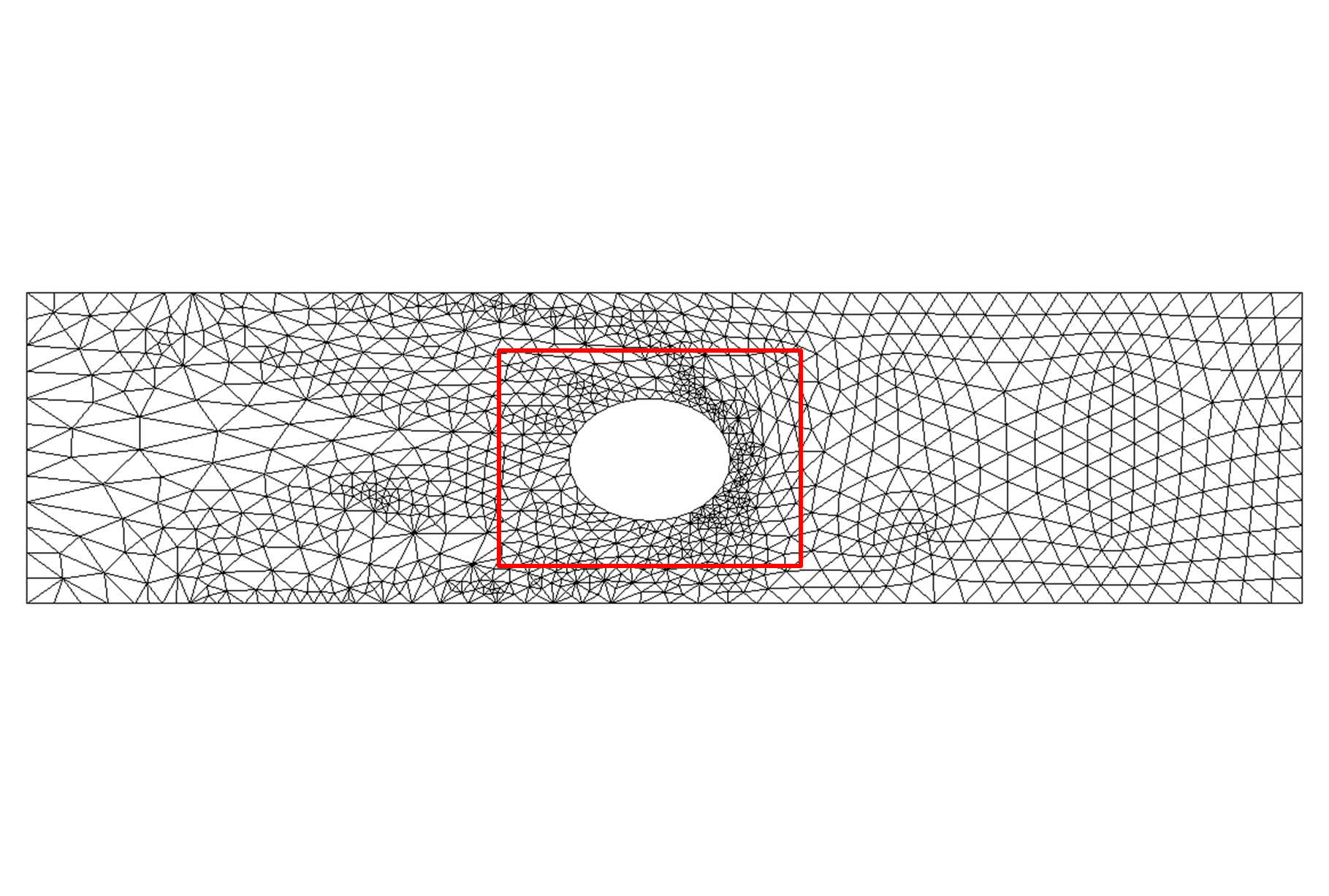
Figure 3: Simulation of the heartbeat cycle using PLBWARP: (a) Initial mesh of the heart; (b) deformed heart mesh using PLBWARP;(c) the DistLU linear solver
is fastest when the triangular factors are reused and a multiple right-hand solver is employed [4]. Joint work
with the authors of [4].
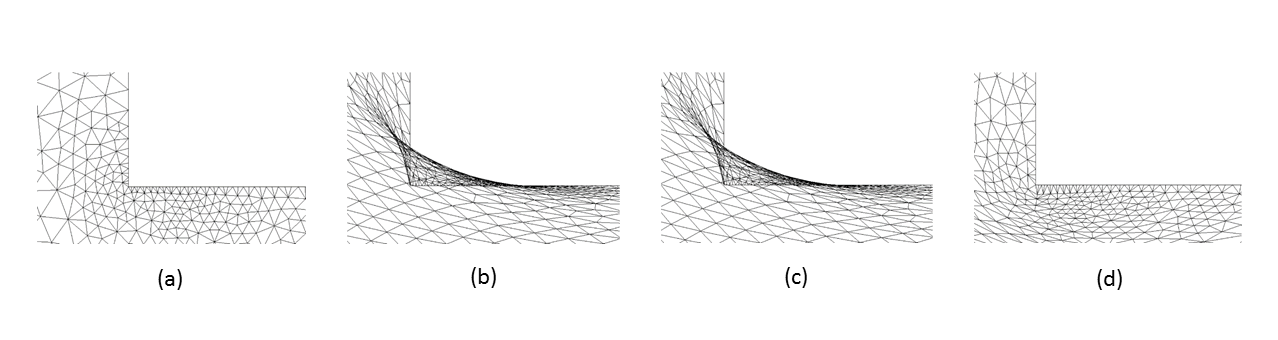
Figure 4: Moving gate meshes (zoomed-in) for an anisotropic boundary deformation aligned with the vertical axis:
(a) Initial mesh on the gate domain; (b) the deformed mesh with FEMWARP;(c) the deformed mesh using anisotropic FEMWARP, and (d) the
optimized mesh on the deformed domain with no inverted elements using the hybrid mesh deformation algorithm [5]. Joint work
with the authors of [5].
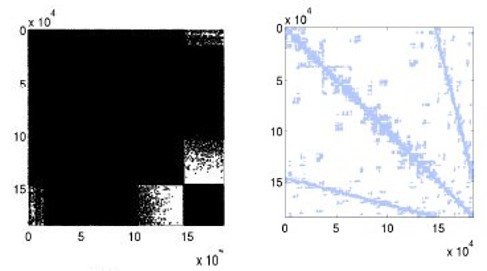
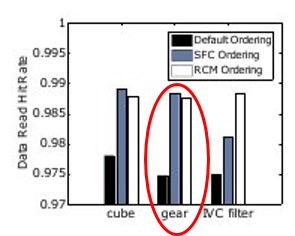
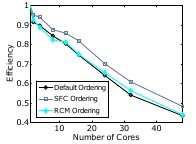
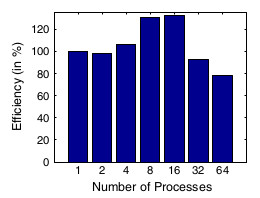
Figure 5: Improved mesh warping performance via (a) Hilbert space-filling
curve mesh vertex and element reordering; (b) improved cache utilization, and
(c) strong scaling efficiency [6]. Joint work with the authors of [6].
-
[7] K.I. Aycock, R.L. Campbell, K.B. Manning, S.P. Sastry, S.M. Shontz, F.C. Lynch, and B.A. Craven,
A computational method for predicting inferior vena cava filter performance on a patient-specific
basis, Journal of Biomechanical Engineering, 136(8):081003, August 2014. ([8] See also the
erratum here.)
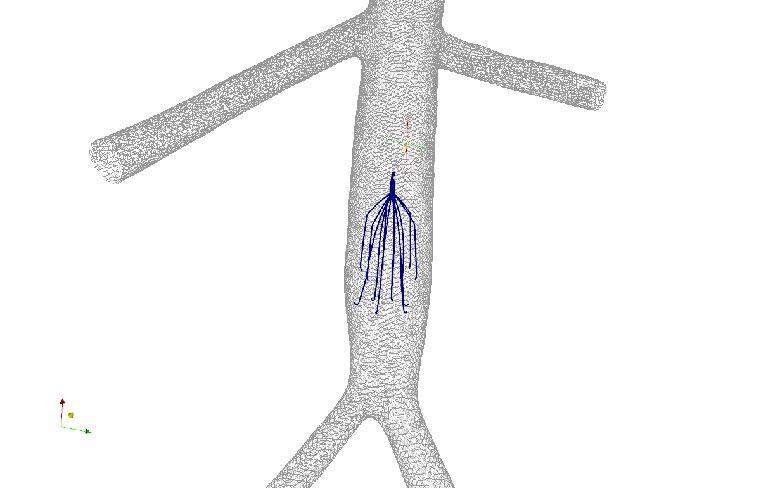
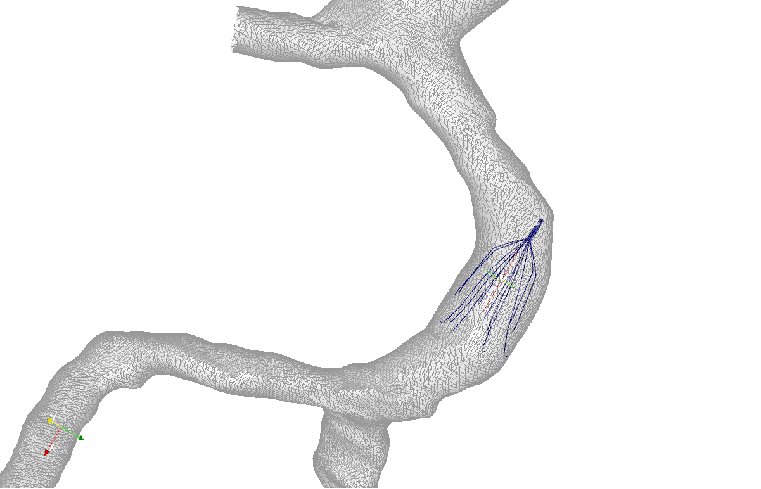
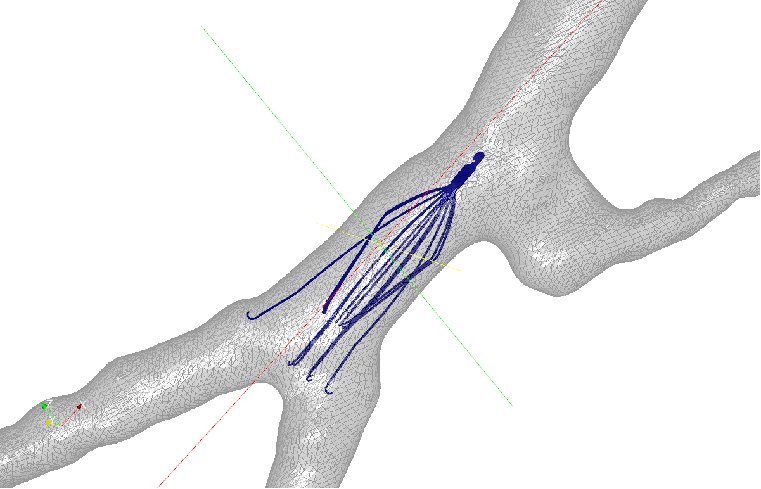
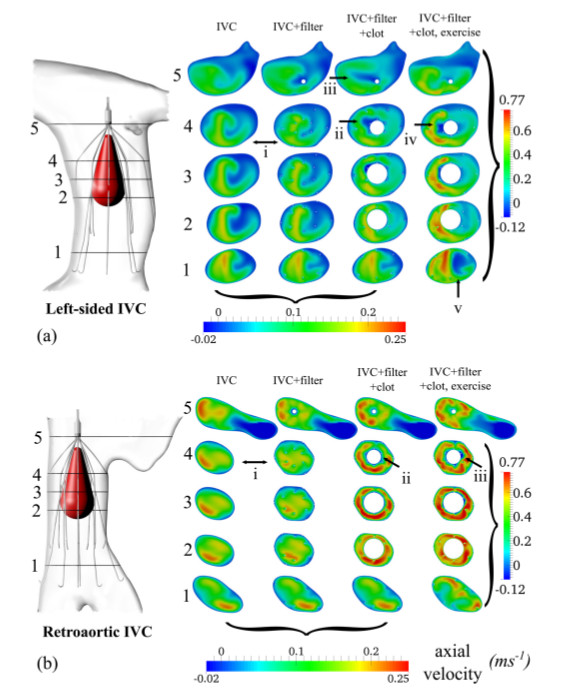
Figure 6: Axial velocity of blood flow in two patient anatomies: (a) a
left-sided IVC and (b) a retroaortic IVC. The four columns represent
the blood flow in the IVC at rest, IVC with IVC filter at rest, IVC with
IVC filter and clot at rest, and IVC with IVC filter and clot at exercise.
Results were obtained at five different cross-sections of the IVC [7].
Joint work with the authors of [7].
Figure 7: Strong-scaling of the parallel log-barrier mesh quality improvement
and untangling algorithm in [9] on a large mesh. Joint work with the authors of [9].
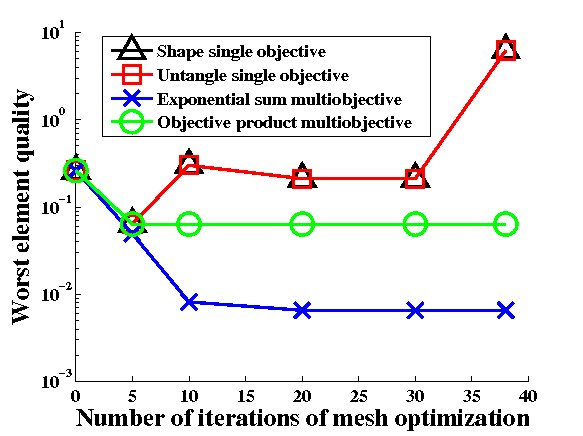
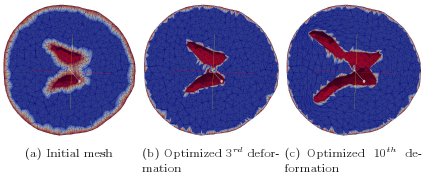
Figure 8: Initial and deformed (tangled) hydrocephalic brain meshes from the authors
of [2]. Comparison of the performance of our multiobjective mesh optimization method with
other mesh quality improvement and mesh untangling methods [10]. Joint work with the authors
of [10].
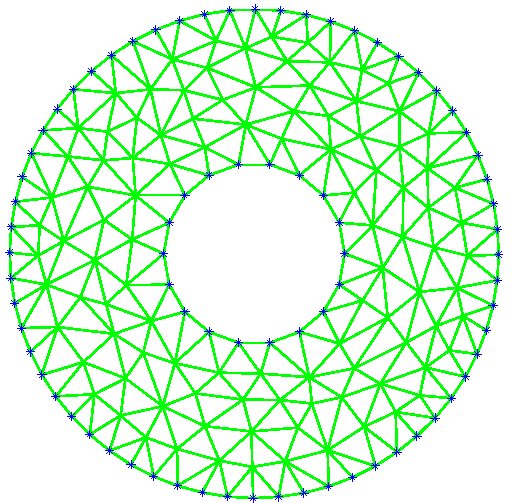
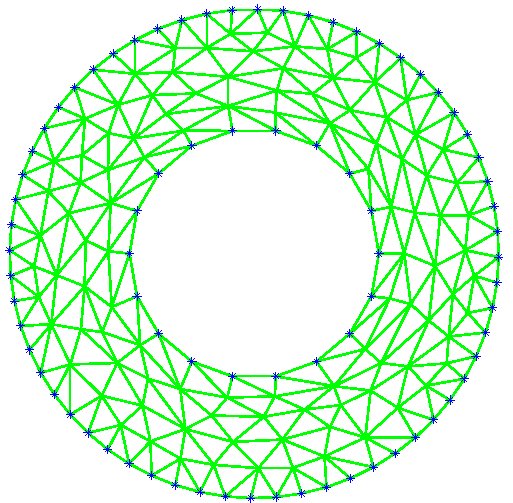
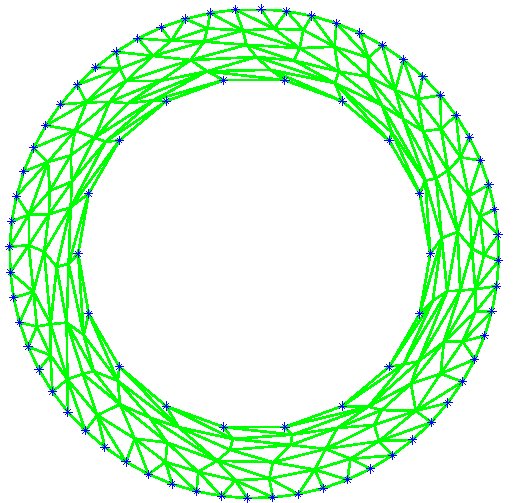
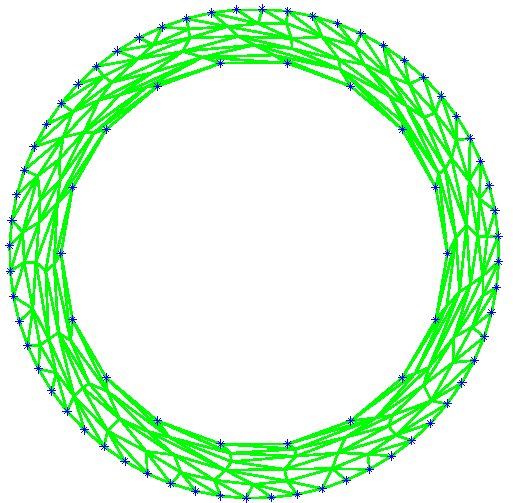
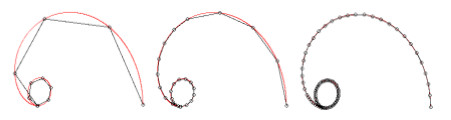
Figure 9: Deformed annulus meshes resulting from the use of our Untangling Before
Newton (UBN) method for rotating the exterior
boundary circle of the mesh shown in Fig. 1 by f radians and moving
the inner boundary circle by a factor f closer to the outer boundary.
The deformed meshes are for (left to right) f = 0.1, f = 0.3, f = 0.6, and
f = 0.7 [11]. Joint work with the authors of [11].
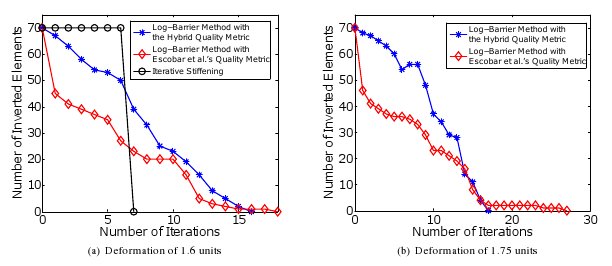
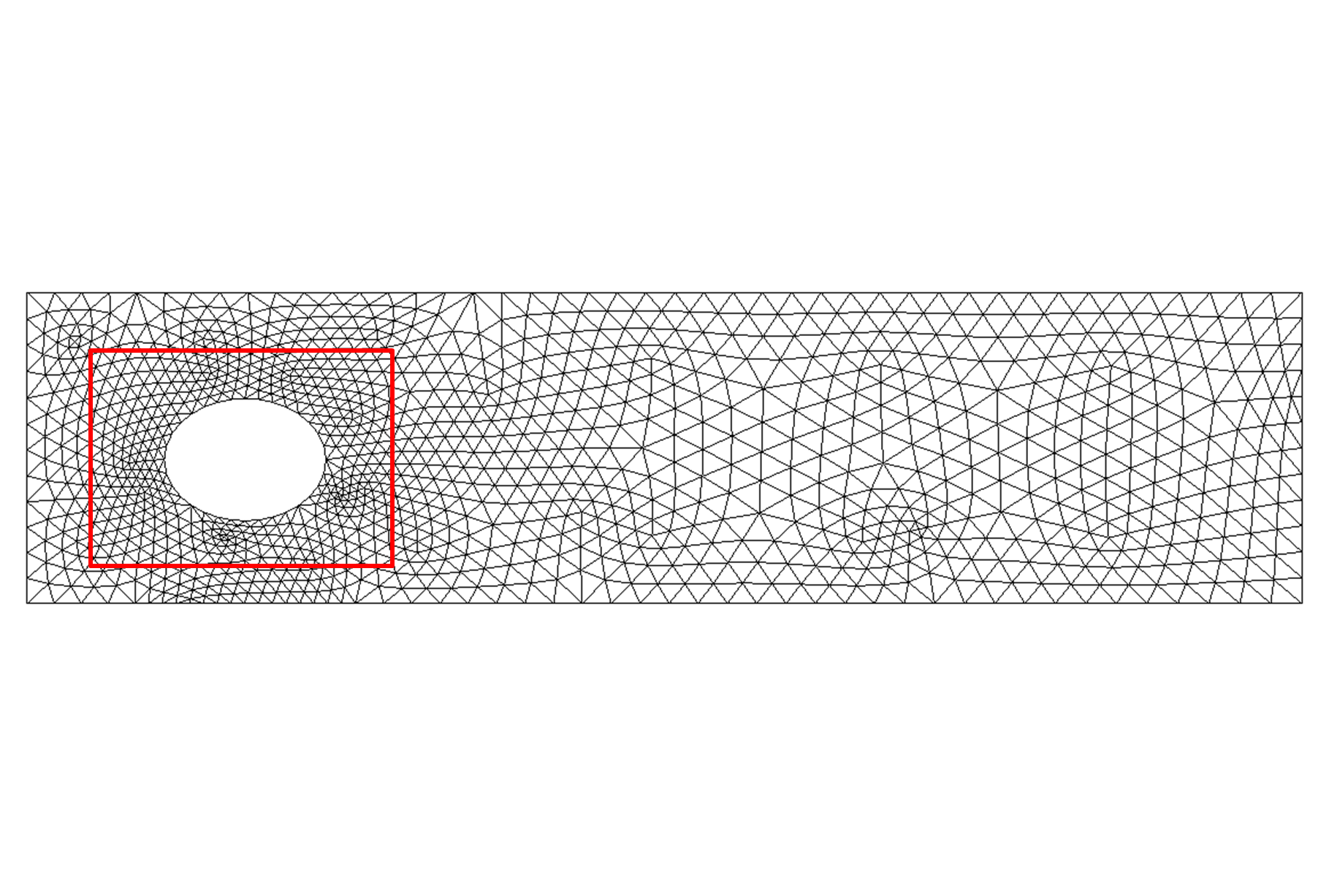
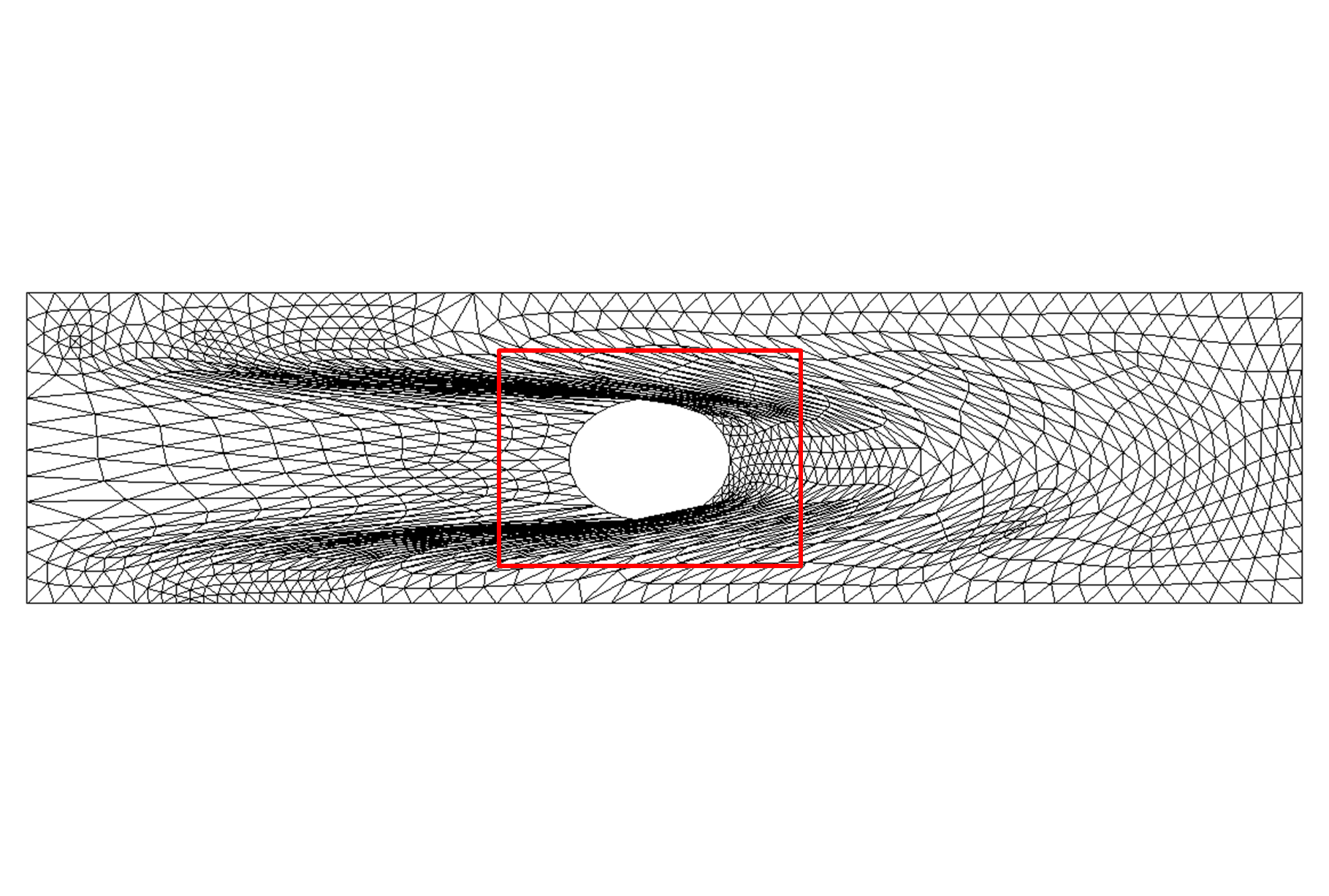
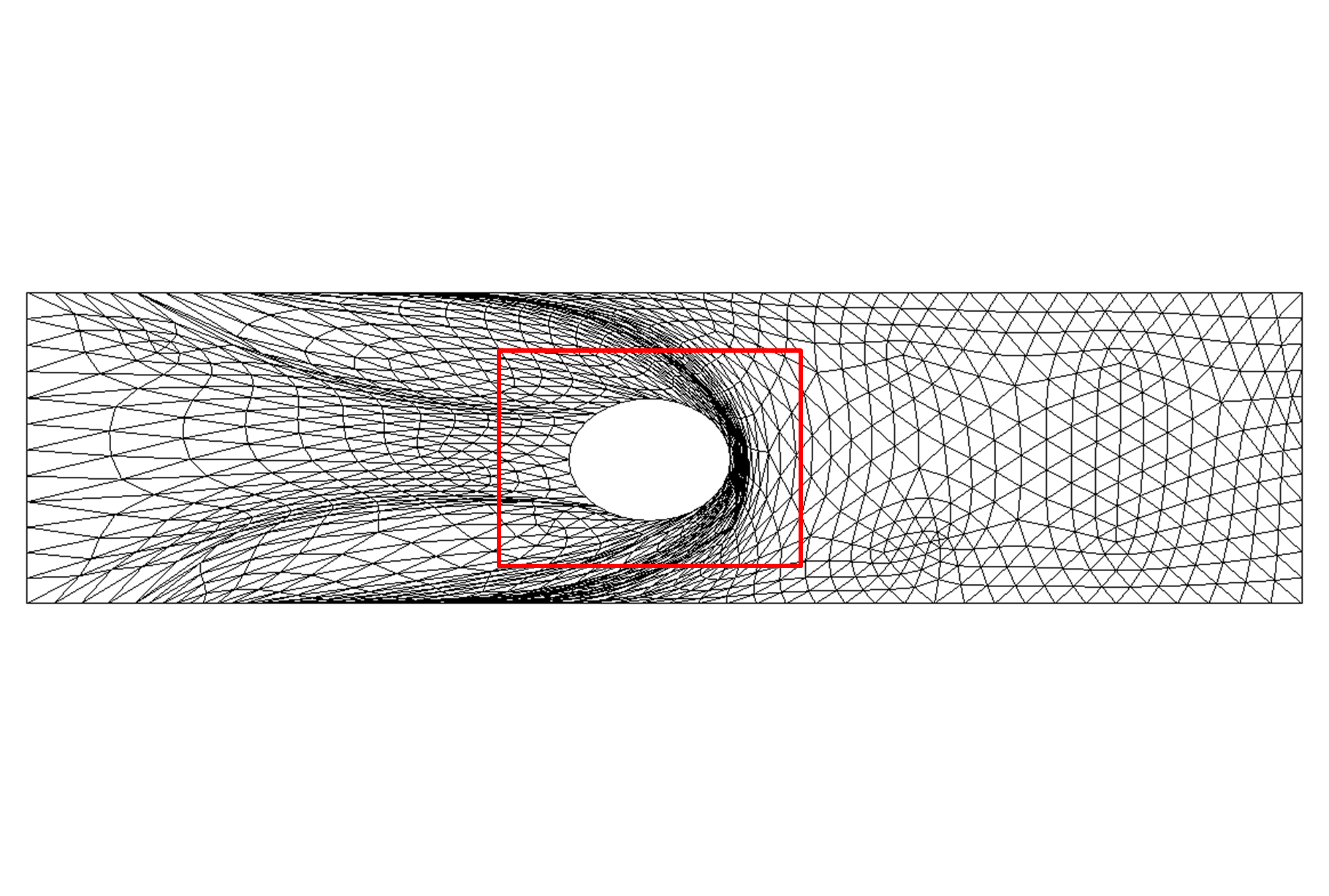
Figure 10: The number of inverted elements after each iteration for all the three methods for the deformation of
1.6 and 1.75 units of the foam5 mesh. Note that only the number of iterations are provided. For 1.75 units of
deformation, the iterative stiffening algorithm does not yield an untangled mesh even after 100 iterations. The
time for untangling cannot be compared because the implementations of the respective algorithms are in different
software environments [12]. Joint work with the authors of [12].
Publications Submitted to Refereed Conference Proceedings:
Publications in Refereed Conference Proceedings:
-
[13] J. Kim, D. McLaurin, and S.M. Shontz, A 2D topology-adaptive mesh deformation framework
for mesh warping, Proc. of the Fourth Tetrahedron Workshop on Grid Generation
for Numerical Computations, Published in New Challenges in Grid Generation and
Adaptivity for Scientific Computing, Volume 5, SEMA SIMAI Springer Series, pp. 261-279,
2015.
Figure 11: Four steps of the hybrid mesh warping algorithm: original mesh;
deformed mesh using anisotropic FEMWARP; untangle mesh using multiobjective
mesh optimization algorithm in [10]; perform edge flips to improve mesh quality,
and perform mesh smoothing in order to further improve mesh quality (read left
to right and top to bottom) [13].
Joint work with the authors of [13].
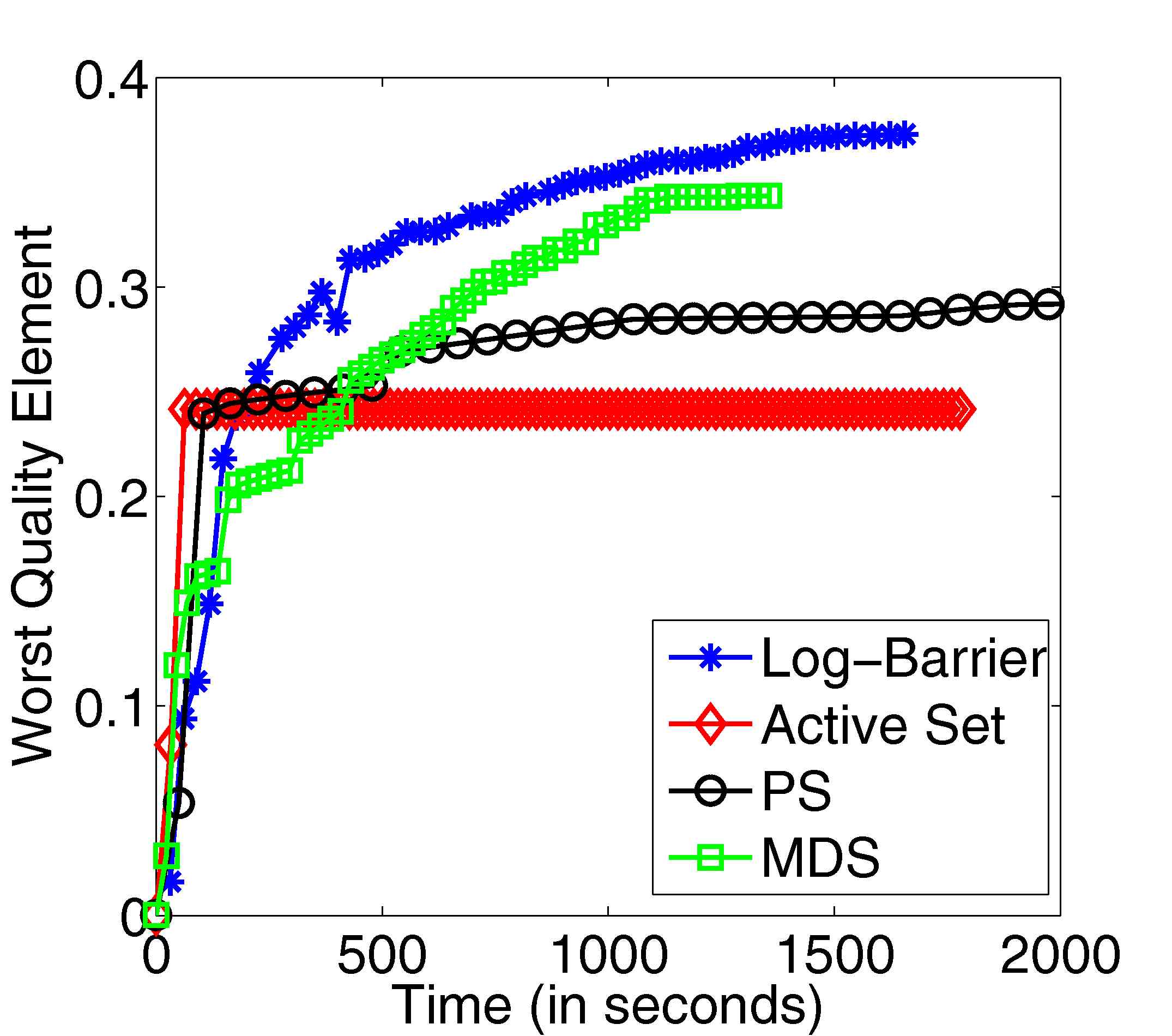
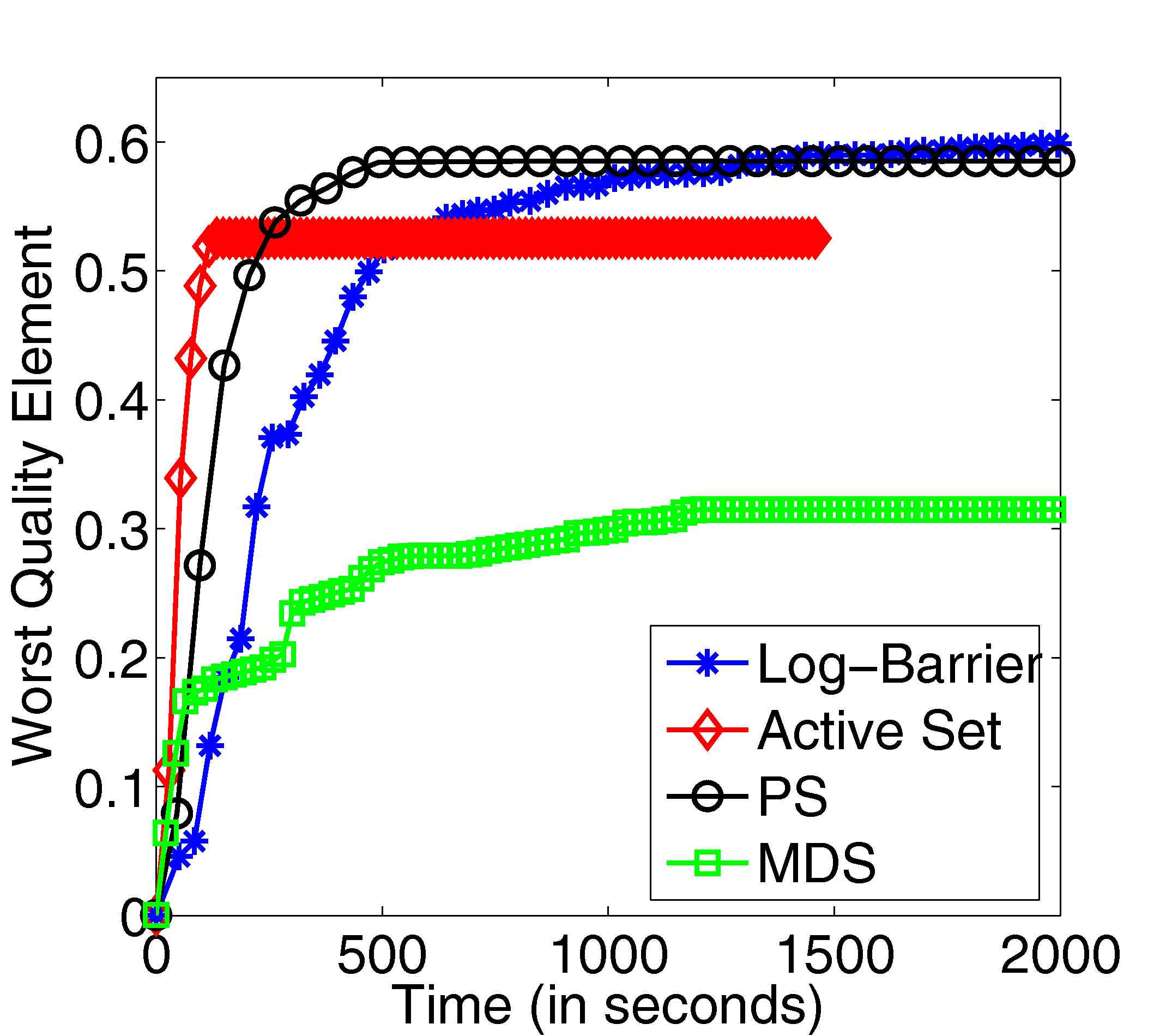
Figure 12: Results from improving the worst quality mesh element using our interior point method.
Comparison with existing worst element mesh quality improvement algorithms in the literature on
a convex mesh optimization problem using a smooth aspect ratio quality metric [14]. Joint
work with the authors of [14].
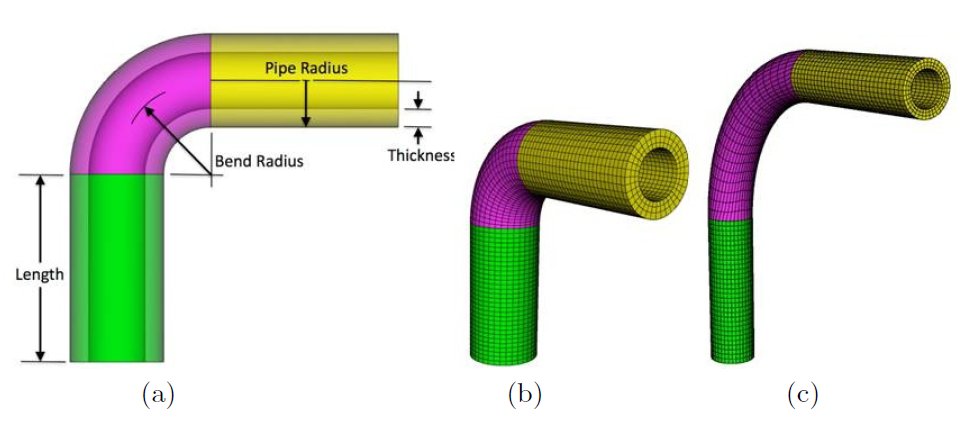
Figure 13: Mesh morphing pipe example [15]. The morphing is performed in conjunction with shape optimization
of the pipe design. Left to right: (a) pipe design and parameters to be optimized, the (b) initial shape,
and the (c) final shape. Joint work with the authors of [15].
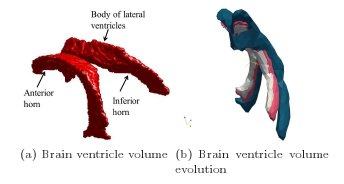
Figure 14a: Development of hydrocephalus [16]: (a) The brain ventricle volume obtained from the segmented 3D MR image.
(b) The brain ventricle volume evolution via the level set method. Joint work with the
authors of [16].
Figure 14b: (a) The mesh having the ventricular boundary vertices matched to the 3D
normal brain MRI. ((b) and (c)) The deformed meshes generated by the FEMWARP
algorithm. Each evolved surface was computed via the 3D level set method with constant
speed of 0.01. The mesh contained 8200 vertices and 40,783 elements. The blue-colored
brain represents the part to be deformed. Mesh quality improvement was performed to
improve the mesh quality at each step of the brain ventricular volume deformation [16]. Joint work with the
authors of [16].
Figure 15: Optimal edge grid generation on a cocheloid curve in 1D [17]. Joint work with the authors of [17].
Ph.D. Dissertations
-
[18] Shankar Prasad Sastry, "Dynamic Meshing Techniques for Mesh Quality Improvement and
Deformation", The Pennsylvania State University, August 2012.
-
[19] Jibum Kim, "Optimization-based Meshing Techniques for Mesh Quality Improvement and
Deformation", The Pennsylvania State University, December 2012.
-
[20] Thap Panitanarak, "Scalable Graph and Mesh Algorithms on Distributed-Memory Systems", The Pennsylvania State University, August 2017. (Thap was co-adivsed with Kamesh Madduri.)
Software Toolkits
Education Results
See [3] above in Research Results for a paper I wrote with numerous other researchers which also
pertains to education in Computational Science and Engineering.
In Fall 2011, I added parallel meshing techniques and biomedical
applications to the graduate level meshing techniques course which I
designed and previously taught in Spring 2008 and Spring 2010 (offered
both times at Penn State). Here are
relevant course materials for Fall 2011 (offered at Penn State):
In Spring 2013, I offered Simulation Modeling, an interdisciplinary,
senior/graduate-level course in mathematical modeling, computational simulation,
and scientific visualization, at Mississippi State. Here are the relevant
course materials:
Simulation Modeling Poster Session, Spring 2013. Photo credit: Mississippi State University.
In Fall 2014, I taught EECS 700: Computer Modeling, Simulation, and Visualization (formerly Simulation Modeling) at the University of Kansas.
The course is now a graduate course, although it is also open to top undergraduate students. Here are the relevant course materials:
In Spring 2016, I taught EECS 801: Numerical Partial Differential Equation and Meshing Techniques as an independent study course at the University of Kansas.
The meshing portion of the course stemmed from previous offerings of CSE 598C at Penn State. Here are the relevant course materials:
Outreach Results
In Summer 2011, I teamed up with Mr. George Otto (Penn State Visualization Group), Dr. Keefe Manning (Penn
State Department of Biomedical Engineering), and Dr. Amy Freeman (Penn State Pre-First Year and
Multicultural Engineering Programs) to offer a workshop to underrepresented entering college freshmen at
Penn State.
Here is a link to (a slightly modified version of) my outreach
presentation on computational biomedical science. This talk is aimed at
entering college freshmen interested in majoring in engineering.
In Summer 2014, I gave outreach presentations on computational biomedical science to the Engineering for Everyone Camp
(10th-12th graders) and the Batmen Camp (middle school boys) at Mississippi State. The students also participated in
a team activity in which they learned about algorithms. The high school students worked on a simple algorithm related
to mesh quality. The middle school boys came up with algorithm pseudocodes for making breakfast.
Here is a link to my outreach presentation at the Batmen Camp.
the talk is aimed at middle school students. My presentation at the Engineering for Everyone Camp for high school students was similar. The difference is that I spent more time explaining the basic concepts and asking students interactive questions when presenting the talk to the middle school students.
We have also given several conference and invited seminar presentations on various aspects of this project.
Return to Suzanne Shontz's Home Page