Stereo Projections: Background, Mathematics, and Use

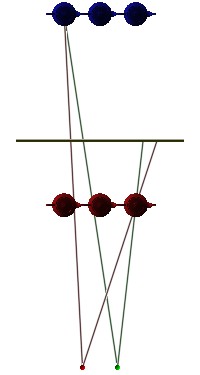
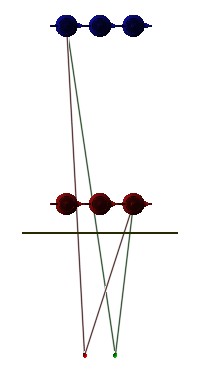
2. Retinal Disparity

When our eyes focus on one point, the relative position of other points will in general project differently in each of our two eyes. These differences allow us to detect whether the other points are nearer or farther away. We first encountered this effect when studying motion parallax earlier in these notes. We examined the image on the top at the left when understanding the different behavior of the teapots during the animated sequence.

You may have noticed the significance that the actual position of the assumed projection plane played. That is, it was really because we positioned the projection plane between the two rows of teapots that they behaved differently during the change of eye positions (i.e., they moved in opposite directions). Yet this is not an artificially created effect.

Hold your finger about eight inches in front of your face. Focus your gaze on your finger and notice what happens to some object (say, a lamp) several feet away. You see two of them! Without moving your finger, focus your eyes on the lamp. After they are fully focused on the lamp, you should now see two fingers in front of your face. The double images that you perceive in each case are the two different images projected on the retina of your left and right eyes. Focusing our eyes on an object forces our eye muscles to rotate our eyes so that the object on which we are focusing projects the same way onto each retina. Objects farther away (or nearer) project differently on the two retinas, and it is these differences (i.e., this retinal disparity) that produces the binocular depth cue so critical to stereo perception.

Changing the position of the projection plane in the example on the left is a way to approximate the effect of our eyes focusing on given objects. For example, to simulate focusing on one of the red teapots, position the projection plane so that it passses through them. Clearly there is then no difference between the left and right generated images of the red teapots. (Well, no difference if we ignore the fact that the teapots have finite size, and hence they actually straddle the plane.)

Alternatively, focusing our eyes on some object in front of the red teapots will actually produce a result different from what we saw in the "motion parallax" section earlier. That is, both rows of teapots will follow the eye as it moves side to side. We can see this by examining the way the teapots project on this nearer projection plane as illustrated in the image on the bottom at the left.