

 |
 |
The two most common shape approximating curves are Bezier and B-Spline curves. The techniques we will see here apply to both. However, the former is a special case of the latter, and it is simpler to introduce the concepts in the context of Bezier curves, so that will be our focus here.
Bezier (and B-Spline) curves can be constructed using the interpolation and shape approximation techniques introduced on the previous page. In addition, there are several editing schemes commonly used with these shape approximating curves. Here we introduce four common techniques for interactive modeling and editing of Bezier curves: piecewise construction, subdivision, degree raising, and degree lowering.
Informal definition: Given a Bezier curve B0 of degree n, create a new Bezier curve B1 of degree m such that B0 meets B1 with Ck (or Gk) continuity for some desired k.
Notes:
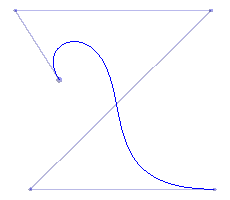
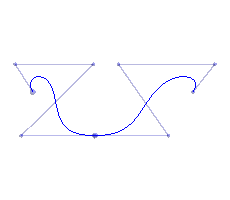
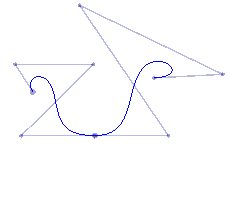
| A degree 4 Bezier curve | We graft a new degree 4 curve with C1 continuity and make some adjustments | Continued adjustment will preserve C1 continuity as long as the points on the bottom are unchanged |
 |
 |
 |
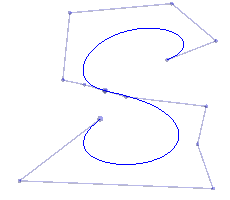
Informal definition: Given a Bezier curve B of degree n and a point in the interior of the curve, create two Bezier curves B0 and B1 – each of degree n – which, when taken together, exactly reproduce the original curve B. B0 starts at the start of B and ends at the common point. B1 starts at the common point and ends at the end of B.
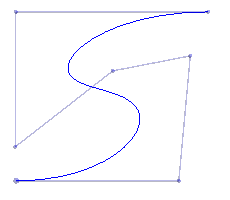
| A degree 6 Bezier curve | The two subdivided degree 6 curves which, taken together, reproduce the original curve | After adjusting the two pieces independently, preserving C1 continuity at their joint | The adjusted curve with the display of the control polygon suppressed |
 |
 |
 |
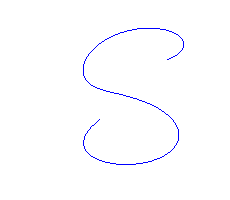 |
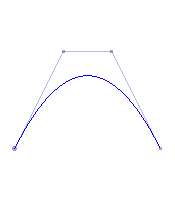
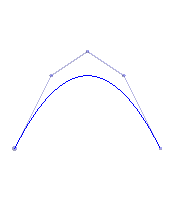
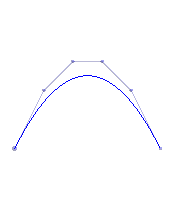
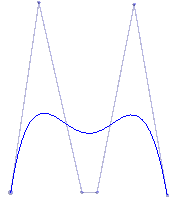
Informal definition: Given a Bezier curve B of degree n, create a Bezier curve B* of degree n+1 which exactly reproduces the original curve B.
| A degree 3 Bezier curve | The same curve represented as a degree 4 Bezier curve | The same curve represented as a degree 5 Bezier curve | After subsequent modification of the curve using its degree 5 representation |
 |
 |
 |
 |
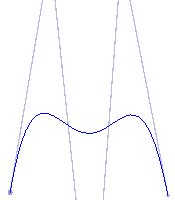
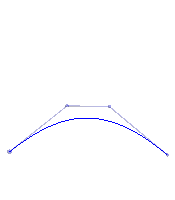
Informal definition: Given a Bezier curve B of degree n, create a Bezier curve B* of degree n–1 which is as close in shape to the original curve B as possible in a least-squares sense.
Note that you actually lose design flexibility with degree lowering. Moreover, unlike the previous techniques, use of this technique will in general result in a change of shape.
The first example in the table shows a nice example in that the curve shape changes very little when the degree is reduced. It illustrates the canonical example of when this technique is useful: when the shape is such that the higher degree is really not needed. By contrast, the second row of the table shows a more extreme example in which the shape changes dramatically when the degree is lowered.
| We start with the degree 5 curve we created when discussing degree raising | We perform a degree lowering operation, getting a least squares best degree 4 approximation. (Note that this curve is now defined with five points – one fewer than the curve on the left – two control points are outside of view above the window, and one is out of view below it.) Changes in the curve are very minor and subtle | Another degree lowering opereration gives us a degree 3 approximation to the original degree 5 curve | One last degree lowering operation leaves us with a degree 2 approximation |
 |
 |
 |
 |
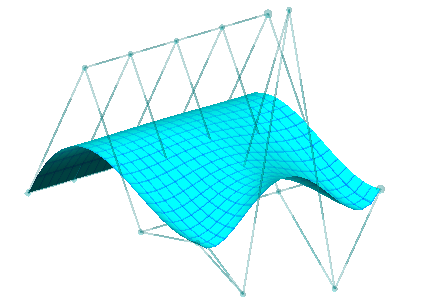
Tensor product surfaces can be defined as a straightforward extension of curves, and curve algorithms typically extend very directly to the tensor product surface domain. For example, a degree n x m Bezier surface is defined using an (n+1) x (m+1) array of control points:
| A degree 4x3 Bezier surface | The surface with its control points and polygon |
 |
 |
 |
 |