EECS 690: M-ary Quadrature Amplitude Modulation


Objective
The goal of this exercise is to correctly demodulate the noisy received signal in Rx16QAM.mat.


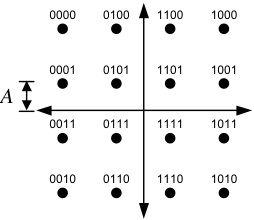
Signal Constellation

The transmitted data points are taken from the signal space constellation below.  The 16 points are arranged into a square pattern with a scale factor of A.  You should be aware of the relationship between A and the average symbol energy.  Each transmitted signal carries four information bits, as shown below.

16QAM Signal Constellation


After being corrupted by noise, the received signal is demodulated by the system below, which detects the transmitted signal space points and outputs the estimated values of the transmitted bits.

Design Exercise

Part I: Generic MQAM Transmitter

Block Diagram of MQAM Modulator

Using blocks from the SIMULINK Block Library, the Signal Processing Blockset, and the Communications Blockset, design a MQAM modulator, patterned after the one shown above, to meet the following specifications:
Number of samples per symbol: 8
Normalized carrier frequency:    0.25 cycles/sample
Pulse shape:                            square-root raised cosine (SRRC) with roll-off = 0.5 and Lp = 6 symbols
Average symbol energy:            40 Joules

As you can see, the above modulator is identical to the QPSK and MPSK modulators.  The only difference between the modulators is the contents of the respective look-up tables.

Part II: Generic MQAM Detector

Block Diagram of MQAM Detector

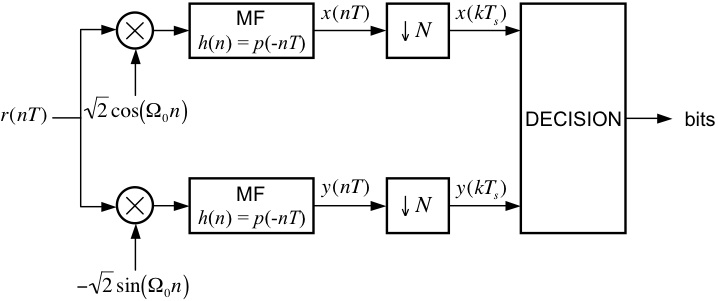
Using blocks from the SIMULINK Block Library, the Signal Processing Blockset, and the Communications Blockset, design a MQAM detector, patterned after the one shown above, that is compatible with the modulator from Part I.  In your implementation, you might find it eaiser to output the signal space projections to the Matlab workspace and implement the decision logic in a post-processing fashion using a Matlab script.


[ Sanity Check ]
You can test your designs from Parts I and II by connecting the output of your modulator to the input of your detector.  The data source (Signal from Workspace block) emits symbol indexes, which are integers in the range 0 to 15.  Set this block to output the four-symbol sequence [9 4 3 14]'.  The I and Q look-up tables convert these indexes to the constellation points.  In your project window, go to the menu Simulation --> Configuration Parameters and set the parameters to:
Start Time:         0.0
Stop Time:          (4+12+1)*8
Solver options:    Type: Fixed-step, Solver: discrete (no continuous states)
Fixed step size:    1
Note: The 4 corresponds to the number of transmitted symbols, the 12 corresponds to the combined delay of the modulator pulse and the detector matched filter, the 1 corresponds to the delay of the downsample operation in the detector, and the 8 is the number of samples per symbol. 

Remember, it is very important that your Downsample block is sampling at the correct "phase".  This may require some adjustment/experimentation on your part.  You want to sample the matched filter outputs so that the samples you keep have the exact same values as the values you transmitted from the look-up tables (since you are running a controlled experiment with no noise, it is possible to get the exact values from the look-up tables).  When you have successfully debugged your system, you are ready for the final part of the exercise.



Part III: Detecting an Unknown Data Set

Here are the steps for the final part of the exercise:
  1. Connect the input of your detector to a From File block and set the filename to Rx16QAM.mat
  2. Set the simulation parameters to:
    Start Time:         0.0
    Stop Time:          (119+12+1)*8
    Solver options:    Type: Fixed-step, Solver: discrete (no continuous states)
    Fixed step size:    1                 
  3. Run the Simulation.
  4. The last 119 values of the sampled matched filter outputs represent 68 ASCII characters.  Determine the message using your own conversion script or an ASCII table, such as the one found here.
  5. E-mail your answer AND your detector model file (.mdl SIMULINK file) plus any additional Matlab code to esp "at" eecs.ku.edu.
  6. Plot the eye diagram and signal space projections.  You do not need to submit these, but they are very helpful in understanding what is going on (as we shall soon see).
Back to the Simulink Exercises Page