Quadrature Phase Shift Keying

EECS 690: Quadrature Phase Shift Keying (QPSK)

Objective
The goal of this exercise is to correctly demodulate the noisy received signal in RxQPSK.mat.

Signal Constellation

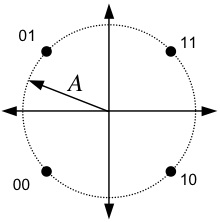
The transmitted data points are taken from the signal space constellation below. The four points are equally spaced on a circle with radius A and are simply the four possible ordered pairs [ ±A/sqrt(2), ±A/sqrt(2) ]. Each transmitted signal carries two information bits, as shown below.

QPSK Signal Constellation

After being corrupted by noise, the received signal is demodulated by the system below, which detects the transmitted signal space points and outputs the estimated values of the transmitted bits.

Design Exercise

Part I: QPSK Transmitter

Block Diagram of QPSK Modulator

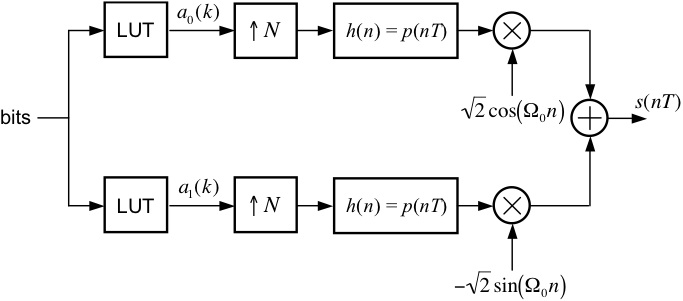
Using blocks from the SIMULINK Block Library, the Signal Processing Blockset, and the Communications Blockset, design a QPSK modulator, patterned after the one shown above, to meet the following specifications:

Number of samples per symbol: 8
Normalized carrier frequency: 0.25 cycles/sample
Pulse shape: square-root raised cosine (SRRC) with roll-off = 0.5 and Lp = 6 symbols

For the purposes of your design, you can omit the bit sequence and the look-up tables (LUTs), and just use two "Signal From Workspace" blocks as inputs to the system.

Part II: QPSK Detector

Block Diagram of QPSK Detector

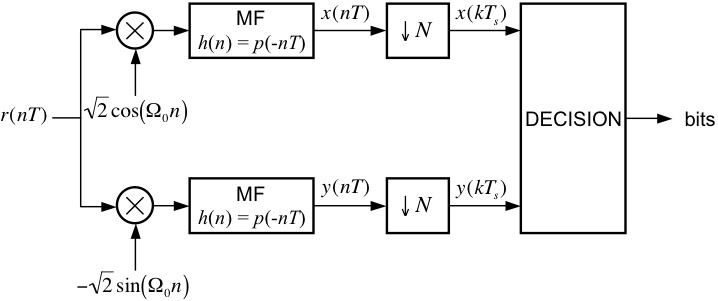
Using blocks from the SIMULINK Block Library, the Signal Processing Blockset, and the Communications Blockset, design a QPSK detector, patterned after the one shown above, that is compatible with the modulator from Part I. In your implementation, you might find it eaiser to output the signal space projections to the Matlab workspace and implement the decision logic in a post-processing fashion using a Matlab script.

[ Sanity Check ]
You can test your designs from Parts I and II by connecting the output of your modulator to the input of your detector. Use the same data source as in the Binary PAM exercise (the Signal from Workspace block), except that you need separate sources for each arm in the modulator. Set the input to these sources such that you modulate the symbol pattern [00 01 10 11]'). In your project window, go to the menu Simulation --> Configuration Parameters and set the parameters to:

Start Time:         0.0
Stop Time:          (4+12+1)*8
Solver options:    Type: Fixed-step, Solver: discrete (no continuous states)
Fixed step size:    1

Note: The 4 corresponds to the number of transmitted symbols, the 12 corresponds to the combined delay of the modulator pulse and the detector matched filter, the 1 corresponds to the delay of the downsample operation in the detector, and the 8 is the number of samples per symbol.

Remember, it is very important that your Downsample block is sampling at the correct "phase". This may require some adjustment/experimentation on your part. You want to sample the matched filter outputs when the magnitude of the value is at a maximum. When you have successfully debugged your system, you are ready for the final part of the exercise.

Part III: Detecting an Unknown Data Set

Here are the steps for the final part of the exercise:

Connect the input of your detector to a From File block and set the filename to RxQPSK.mat
Set the simulation parameters to:
Start Time:         0.0
Stop Time:          (84+12+1)*8
Solver options:    Type: Fixed-step, Solver: discrete (no continuous states)
Fixed step size:    1
Run the Simulation.
The last 84 values of the sampled matched filter outputs represent 24 ASCII characters. Determine the message using your own conversion script or an ASCII table, such as the one found here.
E-mail your answer AND your detector model file (.mdl SIMULINK file) plus any additional Matlab code to esp "at" eecs.ku.edu.
Plot the eye diagram and signal space projections. You can attach the plots to your e-mail message, or turn them in at the beginning of the next class period after the due date.

Back to the Simulink Exercises Page