EECS 690:
Binary Pulse Amplitude Modulation (PAM)
Objective
The goal of this exercise is to correctly demodulate the noisy
received signal in RxBinaryPAM.mat.
Signal Model
The transmitted data points are taken from the signal space
constellation below. Notice the relationship between bits (0, 1)
and symbols (-A, +A).
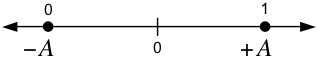
After being corrupted by noise, the received signal is demodulated by
the system below, which detects the transmitted signal space points and
outputs the estimated values. There are two sample rates in the
system below. The
higher sampling rate is 1/T = 16 samples per symbol (indexed by n). The lower sampling rate is 1/Ts =
1 sample per symbol (indexed by k).

Design Exercise
Part I: Binary PAM Modulator
Using blocks from the SIMULINK Block Library, the Signal Processing
Blockset, and the Communications Blockset, design a modulator (below)
for the system model above. Use the modulator to send the
sequence 1 -1 -1 1.

The modulator is composed of four blocks. The first block can be
found at
DSP
Blockset --> DSP Sources --> Signal From Workspace
Drag this block to your project window. Double-click on the
Signal From Workspace block and set the block parameters as shown in
the picture below.
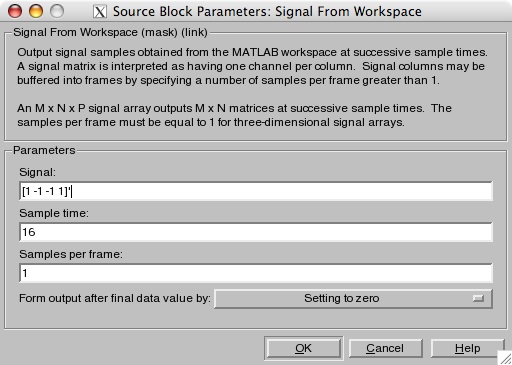
The first parameter is a column vector containing the data to be
modulated. The second parameter specifies the sample time (not rate), which is 16 at
this point in the system. We leave the third parameter
alone. The last option (in the drop-down list) indicates what we
want to happen when the data runs out but the simulation is still
running. We don't care about this since we will set the
simulation time to match the length of the data.
The second block can be found at
DSP
Blockset --> Signal Operations --> Upsample
Drag this
block to your
project window. Double-click on the Upsample block and
set the block parameters as shown in the picture below.
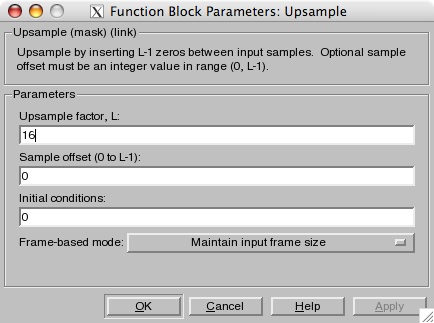 d
d
The first parameter is the upsample factor, which is the number of
samples per symbol. The second parameter is an offset which we do
not need to use (at least in the modulator). Leave it set to the
default of zero.
The third block can be found at
Simulink --> Discrete --> Discrete Filter
Drag this
block to your
project window. Double-click on the Upsample block and
set the block parameters as shown in the picture below.
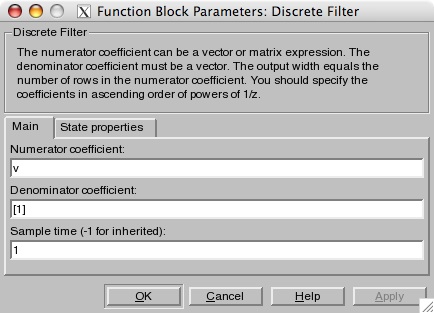 e
e
This block serves as the pulse shaping filter in the modulator.
We want an FIR filter, so we set the numerator to the value of the
filter coefficients, and we set the denominator to the trivial vector
of[1]. For the filter coefficents, you can either
1) type sqrt(1/16)*ones(1,16)
into the Numerator coefficient box itself, or
2) type v=sqrt(1/16)*ones(1,16)
at the Matlab prompt (this
makes the images look a little better).
You will recognize this pulse as the NRZ shape sampled at 16 sample per
symbol. The third parameter is the sample time, which is 1 at
this point in the system.
Now, test your modulator by connecting the output to the Scope block
(this can be found at Simulink --> Sinks). In your project
window, go to the menu Simulation --> Configuration Parameters and
set the parameters to:
Start
Time: 0.0
Stop Time: 80.0
Solver options: Type: Fixed-step, Solver: discrete
(no continuous states)
Fixed step size: 1
Note: We have to run the
simulation for 5x16 samples instead of 4x16 samples since the upsample
block inserts a 16 sample delay. After you go to Simulation
--> Run, the output of the scope (double-click the scope) should
look like this:
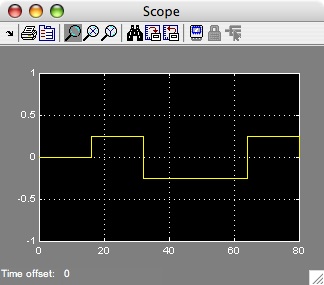
Part II: Binary PAM Detector
Design and build a system in SIMULINK that is based on the block
diagram of the binary PAM detector shown at the top of this
exercise. The SIMULINK experience you have just gained should
prove helpful in this effort.
You can test your detector by connecting its input to the output of
your modulator. Connect the output of your detector to a To
Workspace block (this can be found at Simulink --> Sinks, open the
Properties and set the Save format to matrix, or array). After
running the simulation, a plot of the matched filter output should look
like this:
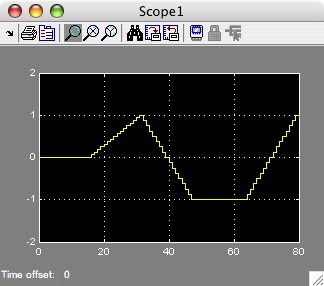
You can see with this test input signal (based on the data 1 -1 -1 1), the first valid
bit decision occurs at sample 32. The others occur at samples 48,
64, and 80. In the Matlab workspace (the Matlab prompt) you will
likely find 6 bit decisions instead of 4. This is because the
Downsample block outputs a value at sample 0 and sample 16. These
two extra values can be ignored.
It is important that your Downsample block is sampling at the correct
"phase". This will require some adjustment/experimentation on
your part. You want to sample the matched filter output when the
value is exactly +1.0 or -1.0 (think of the eye diagram). You may
need to run the simulation to a stop time of 6*16.0, depending on the
sampling offset you use. When you have successfully debugged your
system, you are ready for the final part of the exercise.
Part III: Detecting an Unknown Data Set
Here are the steps for the final
part of the exercise:
- Replace the modulator blocks with the From File
block (found at Simulink --> Sources) and set the filename to RxBinaryPAM.mat
- Set the simulation
parameters to:
Start
Time: 0.0
Stop Time:
16*(7*10+1)
Solver options: Type: Fixed-step, Solver: discrete
(no continuous states)
Fixed step size: 1
- Run the Simulation.
- The last 70 values of
the detector output (you will have to convert +/-1s to 1s and 0s)
represent 10 ASCII characters, with 7 bits per character.
Determine the message using your own conversion script or an ASCII
table, such as the one found here.
- E-mail your answer AND
your detector model file (.mdl SIMULINK file) to esp "at" eecs.ku.edu.
- Plot the eye diagram
and signal space projections. You can attach the plots to your
e-mail message, or turn them in at the beginning of the next class
period after the due date.
Back to the Simulink
Exercises Page
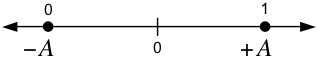



 d
d e
e
