Working With a Parabola

Background

Purpose

This page is intended to provide a quick introduction to the use of the cryph software utilities by showing a couple of realistic examples involving a parabola. First, relevant mathematical formulas are presented or derived, then you will see how the mathematics translates directly to C++ code using the cryph data types AffPoint (a point in a 3D affine space) and AffVector (a 3D vector in the vector space associated with the affine point space).

It is not necessary that you fully understand points and vectors in affine spaces. You need only recall: (i) a point is a position in 3D space, (ii) a vector is an offset in 3D space, (iii) subtracting two points yields the vector that is the offset from one to the other, (iv) a dot product of two vectors yields a floating point number that is the product of the two vector lengths with the cosine of the angle between them, and (v) a cross product of two vectors is a vector perpendicular to both of them.

The Parabola

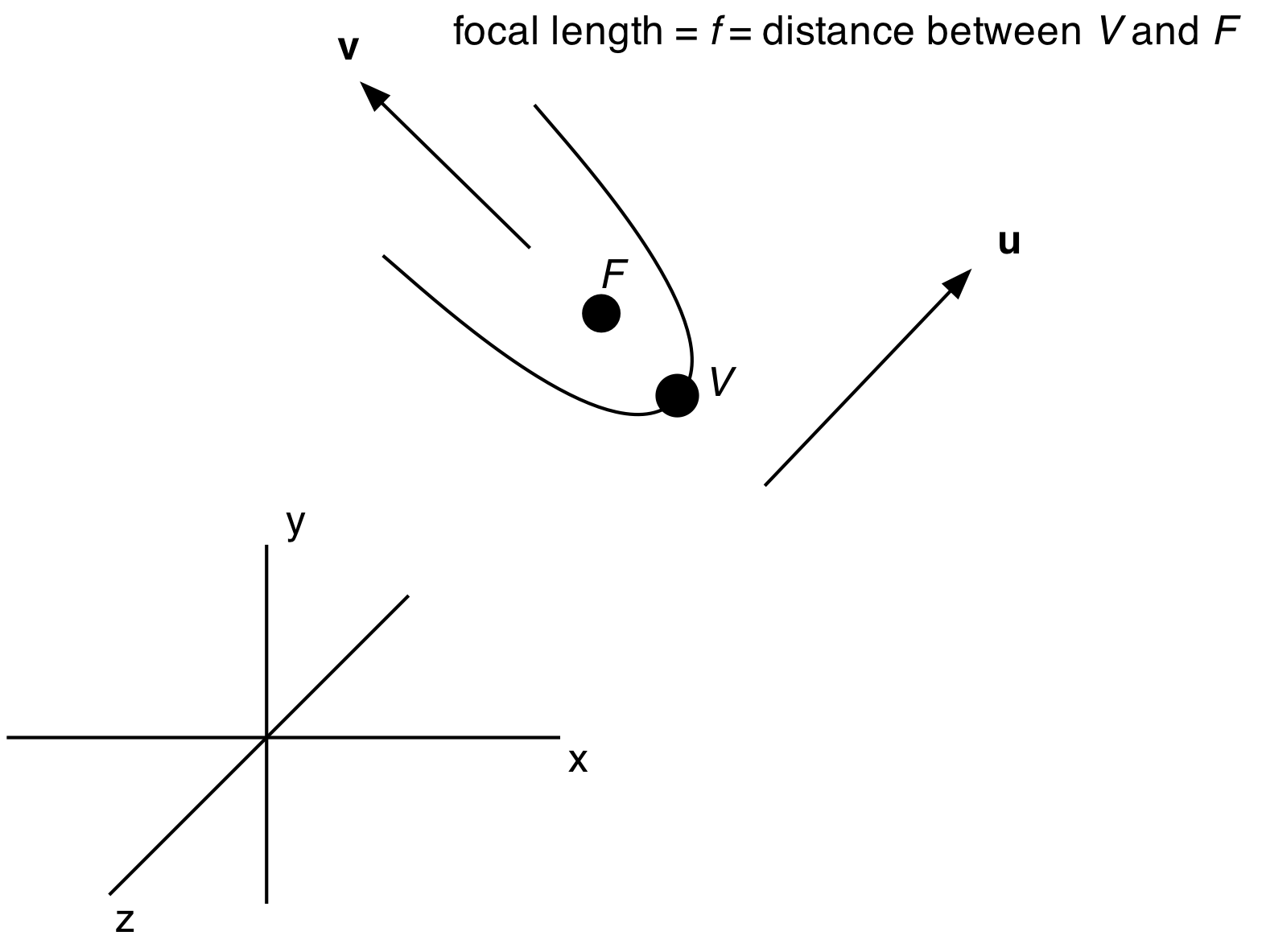
The picture on the right shows a parabola in some arbitrary position and orientation in 3D space. Such a parabola can be uniquely defined by:

There is a one-to-one mapping of real numbers to points on the parabola. The point on the parabola corresponding to the real number t is:

V + 2ftu + ft2v ; -∞ ≤ t ≤ +∞

The point corresponding to t=-∞ is infinitely far away along the left-hand side of the parabola; as t increases, the point slides down the left branch. The vertex is at t=0 (obvious from the formula). Then as t increases through the positive numbers towards +∞, the point continues to march towards infinity along the right-hand side of the parabola.

We often write P(t) to denote a generic point on the parabola corresponding to the real number t:

P(t) = V + 2ftu + ft2v

Drawing a (Piecewise Linear Approximation of) a Portion of the Parabola

Suppose we want to draw a finite piece of a parabola from t=tMin to t=tMax. Using the cryph tools, we can generate a series of points in an array to be sent to the GPU as follows. For simplicity, we are assuming all parameters are valid and that numPoints (the number of points along the parabola we wish to generate) is at least 2. Note also for all examples on this page, the following two header files are required: 

#include "AffPoint.h"
#include "AffVector.h"

cryph::AffPoint* pwlApproxOfParabola(
    // The parabola:
    cryph::AffPoint V,
    cryph::AffVector uHat, cryph::AffVector vHat, double f,
    // The portion of the parabola we wish to draw:
    double tMin, double tMax, int numPoints)
{
    cryph::AffPoint* pnts = new cryph::AffPoint[numPoints];
    double dt = (tMax - tMin) / (numPoints - 1);
    double t = tMin;
    for (int i=0 ; i<numPoints ; i++)
    {
        // Implement: P(t) = V + 2ftu + ft2v
        pnts[i] = V + 2.0*f*t*uHat + f*t*t*vHat;
        t += dt;
    }
    return pnts;
}

Assuming that a buffer name has been generated and bound, the caller of "pwlApproxOfParabola" can then send the data to the GPU in either of the following equivalent ways: 

void sendToGPU_AsFloatArray(cryph::AffPoint* points, int numPoints)
{

    float* ptsAsFloat = new float[3*numPoints];

    for (int i=0 ; i<numPoints ; i++)
        points[i].aCoords(ptsAsFloat, 3*i);

    int numBytes = 3 * numPoints * sizeof(float);
    glBufferData(GL_ARRAY_BUFFER, numBytes, ptsAsFloat, GL_STATIC_DRAW);
    // DON'T FORGET glVertexAttribPointer & glEnableVertexAttribArray
    // Invoke them either here or in caller.

    delete [] ptsAsFloat;
}

void caller()
{
    …
    cryph::AffPoint* pts = pwlApproxOfParabola(V, u, v, f,
        tMin, tMax, numPoints);
    // Make sure a buffer name has been generated and bound, THEN:
    sendToGPU_AsFloatArray(pts, numPoints);
    // DON'T FORGET glVertexAttribPointer & glEnableVertexAttribArray
    // Invoke them either here or in sendToGPU_AsFloatArray.
    delete [] pts;
    pts = NULL;
    …
}
 
void sendToGPU_AsVec3Array(cryph::AffPoint* points, int numPoints)
{
    typedef float vec3[3];
    vec3* ptsAsVec3 = new vec3[numPoints];

    for (int i=0 ; i<numPoints ; i++)
        points[i].aCoords(ptsAsVec3, i);

    int numBytes = numPoints * sizeof(vec3);
    glBufferData(GL_ARRAY_BUFFER, numBytes, ptsAsVec3, GL_STATIC_DRAW);
    // DON'T FORGET glVertexAttribPointer & glEnableVertexAttribArray
    // Invoke them either here or in caller.

    delete [] ptsAsVec3;
}

void caller()
{
    …
    cryph::AffPoint* pts = pwlApproxOfParabola(V, u, v, f,
        tMin, tMax, numPoints);
    // Make sure a buffer name has been generated and bound, THEN:
    sendToGPU_AsVec3Array(pts, numPoints);
    // DON'T FORGET glVertexAttribPointer & glEnableVertexAttribArray
    // Invoke them either here or in sendToGPU_AsVec3Array.
    delete [] pts;
    pts = NULL;
    …
}

Note:

  1. ptsAsFloat and ptsAsVec3 have identical memory layouts - as they must - since glBufferData cannot tell what was passed as its third parameter. Use whatever approach suits you better.
  2. The two "sendToGPU_" routines are completely generic and can be used any time you have created an array of AffPoint instances to be sent to the GPU.

Other Things We Can Do With a Parabola

Finding the parameter of a point on the parabola

Suppose I know that some point, Q, is on the parabola, and I want to know the parameter, tQ, corresponding to that point. I could try to solve the following equation for t:

P(t) = Q = V + 2ftu + ft2v

But that is very unsatisfying because (i) it is actually three equations (one each for the x, y, and z coordinates; more on that takes us too far afield for now); and (ii) they are quadratic equations which means I will in general get two solutions for each equation, only one of which will be common across all three and be the one I want. (Again, let's not worry about what the other solutions are.)

So what can we do that is better? Consider the following algebraic manipulations of the immediately preceding equation.

Q - V = 2ftu + ft2v -------> Still three equations
(Q - V) · u = 2ft(u · u) + ft2(v · u) -------> Dot both sides with u yielding one equation

Since u is perpendicular to v, the second term on the right-hand side is identically zero! That kills the quadratic term, leaving us with a single linear equation. Moreover, since u and v are unit vectors, (u · u)≡1. Hence we are left with:

(Q - V) · u = 2ft

Which means:

tQ = ((Q - V) · u) / 2f

This final expression for tQ can be coded using the cryph utilities as follows. 

double paramterOf(cryph::AffPoint Q, cryph::AffPoint V,
    cryph::AffVector uHat, cryph::AffVector vHat, double f)
{
    cryph::AffVector QminusV = Q - V;
    return QminusV.dot(uHat) / (2.0*f);
}

Generating the description of a parabola from other data

A parabola can also be uniquely defined via:

We can compute the parameters we originally introduced above from these values as follows:

v = normalize(F - V)
u = normalize(v × n)
f = |F - V|

(f is the distance between F and V; equivalently it is the length of the vector (F - V).)

A cryph-based routine to convert the (V, F, n) representation to the (V, u, v, f) representation introduced above can then be written as:

void toStandardForm(cryph::AffPoint V, cryph::AffPoint F, cryph::AffVector n,
	cryph::AffVector& uHat, cryph::AffVector& vHat, double& f)
{
    cryph::AffVector FminusV = F - V;
    FminusV.normalizeToCopy(vHat);
    uHat = vHat.cross(n)
    uHat.normalize();
    f = FminusV.length();
}

There are several other ways this code could be written, some shorter than what I have presented above. As you learn the toolkit, see if you can find alternate ways to code this.

What's Next?

If you want to learn more about the cryph toolkit, see the cryph documentation web pages. As stated there, the documentation is sadly not up-to-date. However, there is sufficient detail and examples so that you should be able to consult the open source implementation (in particular, the header files) to deepen your understanding of how to use the toolkit.