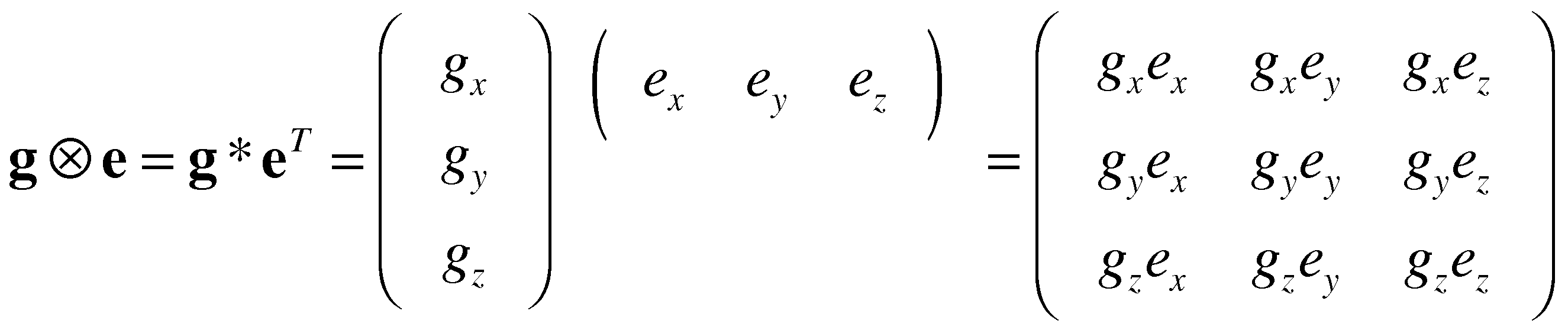Important Operations Defined For
3D Geometric Vectors
Basic Concepts, Terminology, and Notation
- A 3D geometric vector is uniquely determined by a
direction and a length. (For the rest of this page, "vector"
will be used as a shorthand notation for "3D geometric vector".)
- We will use lower case bold letters to denote vectors: a, b, u.
- The notation |a| will be used to denote the length of the vector a.
- Vectors with length 1 are called unit vectors and will be written with a "hat": ê, û.
- A unit vector with the same direction as an arbitrary vector is obtained by
dividing the vector by its length:
ê = normalize(e) = e / |e|. As with
all valid point and vector expressions of this sort, they are applied component-wise.
Hence, if e = (ex, ey, ez),
then:
ê = (ex / |e|, ey / |e|,
ez / |e|)
Dot Product: a·b
The dot product of two vectors is a scalar.
| | Mathematical Definition |
Computational Definition |
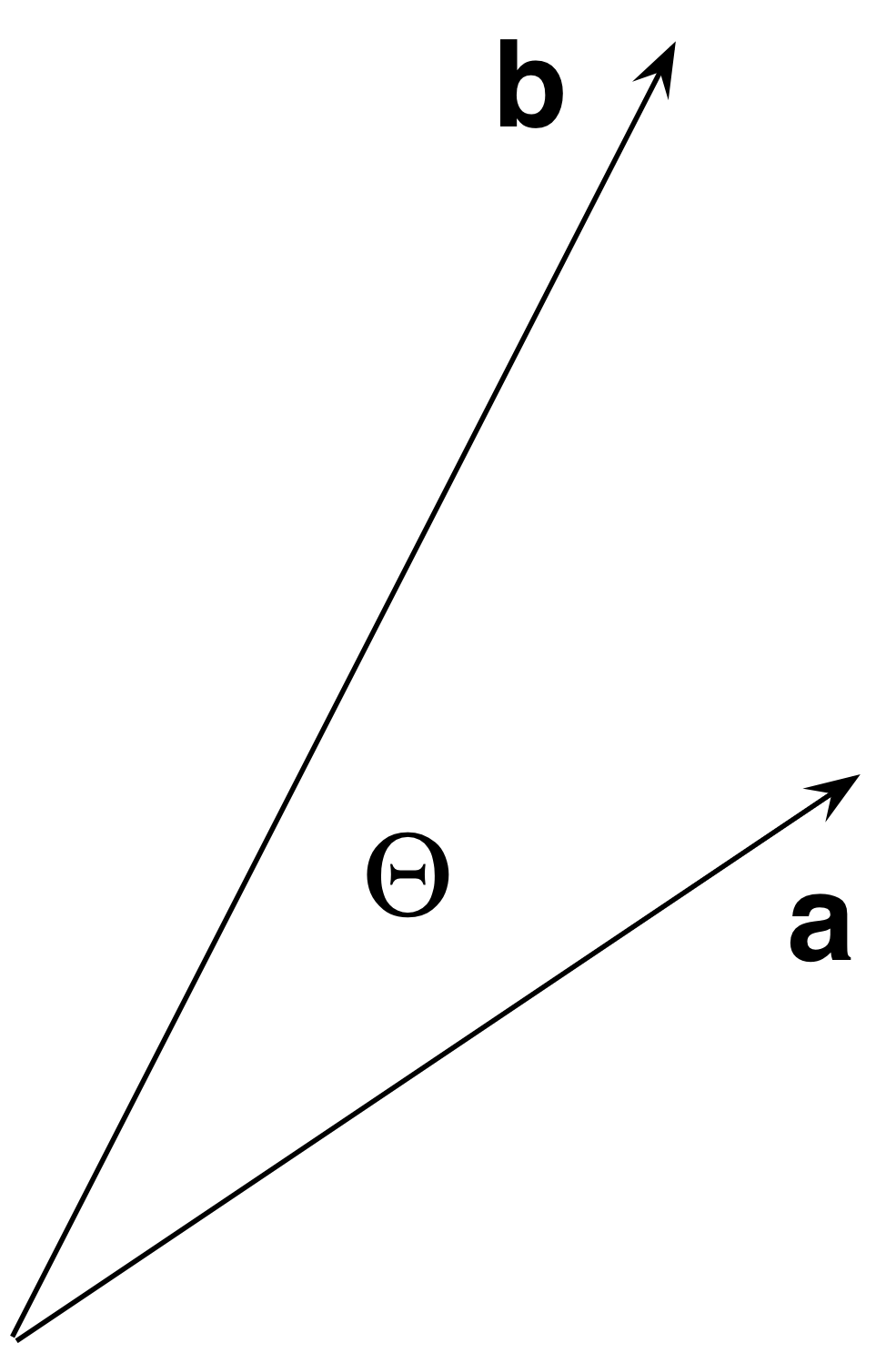 |
a·b = |a| |b| cosΘ |
a·b = axbx + ayby + azbz |
Applications
|
- Computing the length of a vector: |a| = √(a·a)
- Normalize a vector: ê = normalize(e) = e / |e|.
- Using the properties of the dot product (but not the dot product itself),
determine some vector perpendicular to a given vector. (There are an infinite
number of such vectors; how can you find one?)
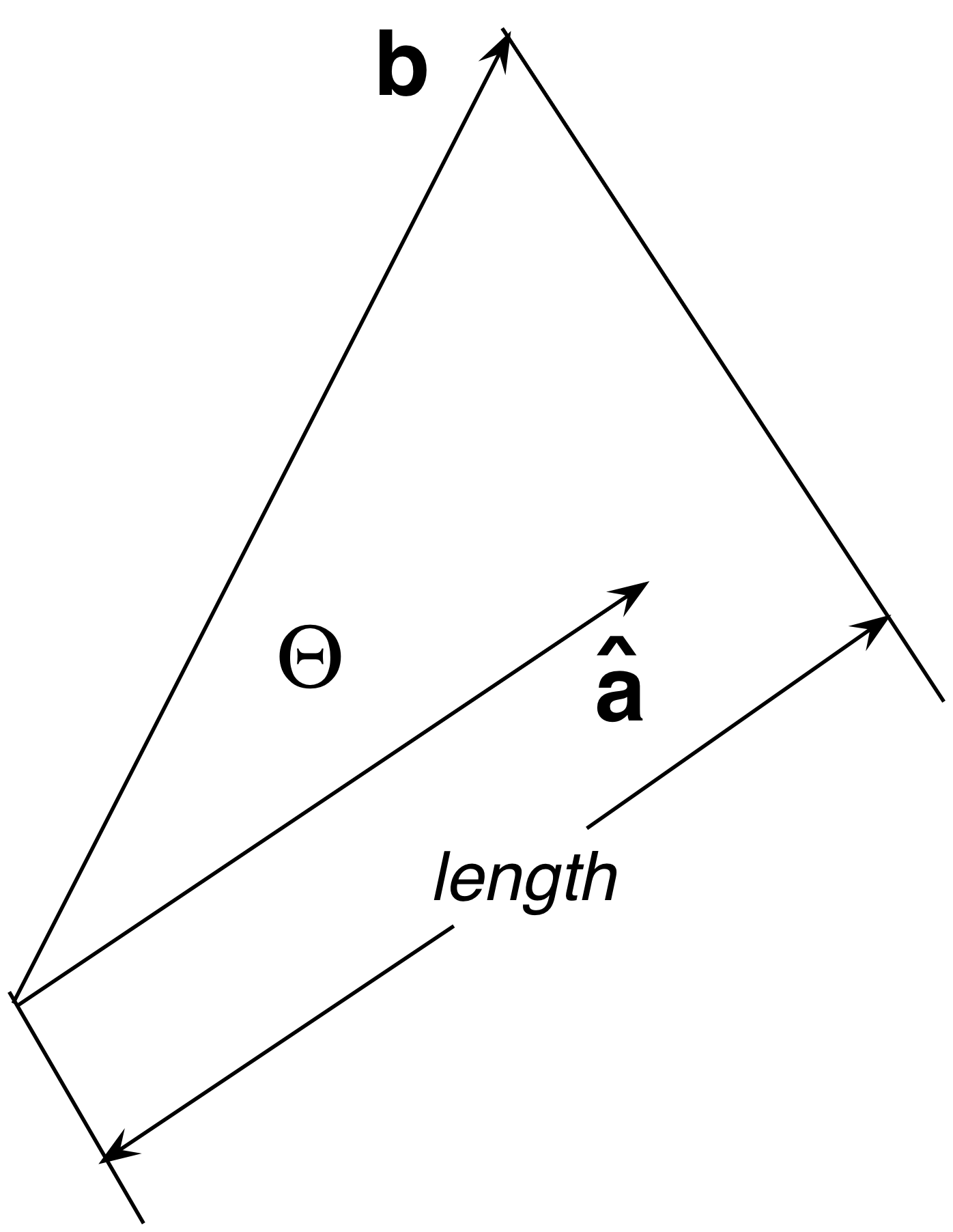
- Compute the length of one vector in the direction of another (unit) vector:
length = â·b.
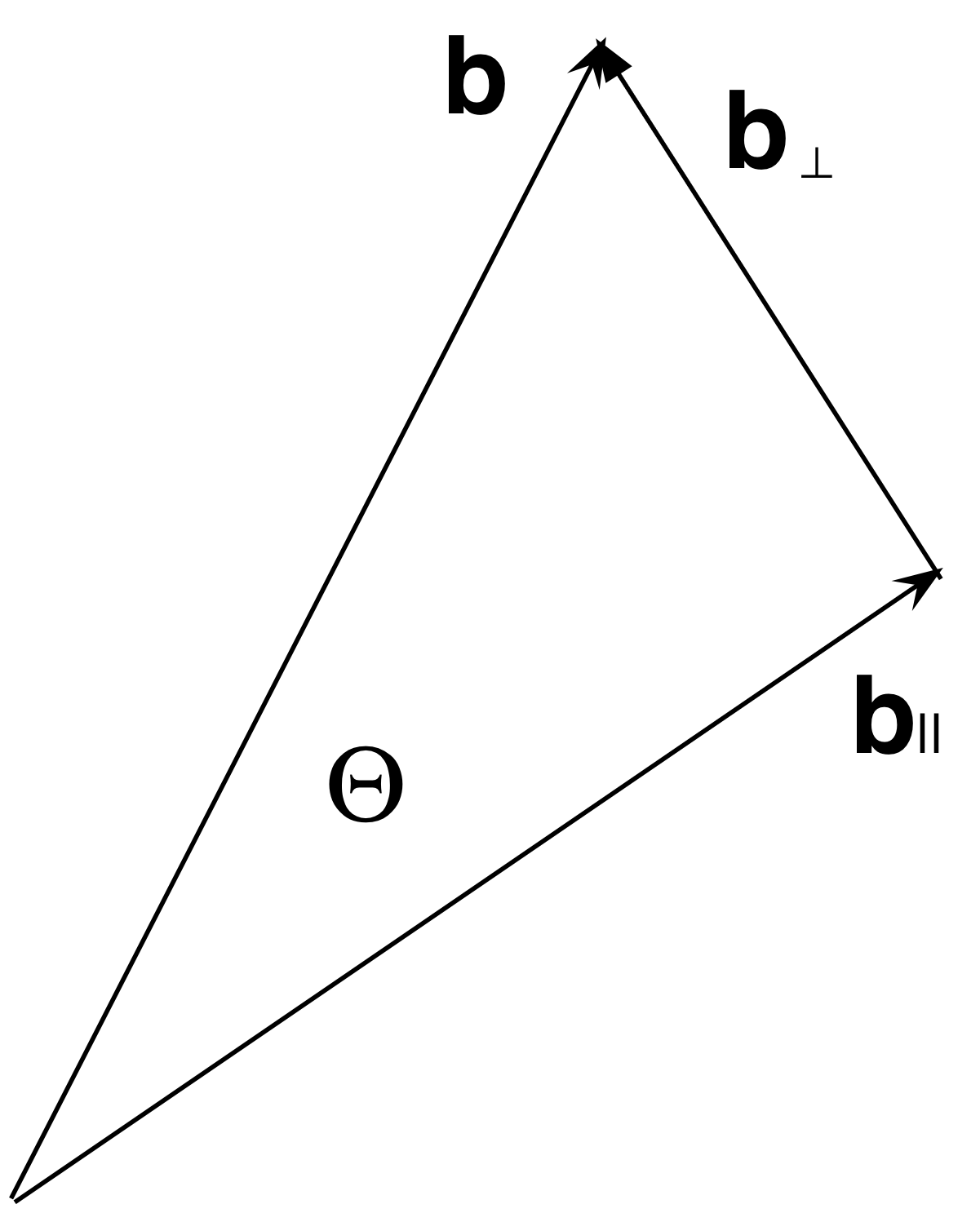
- Using #4, decompose b into its components parallel to and perpendicular to â. That is:
b = b|| + b⊥
where
b|| = (â·b)â, and
b⊥ = b - b|| = b - (â·b)â
|
|
The vector with respect to which the decomposition is done is usually clear from
the context. If there is a potential for confusion, we will write:
b||,â and b⊥,â.
Observations
- Computing the dot product of two 3D vectors is equivalent to multiplying a
1x3 matrix by a 3x1 matrix. That is, if
we assume a represents a column vector (a 3x1 matrix) and aT represents a row vector (a 1x3 matrix), then we can write:
a · b = aT * b
- Similarly, multiplying a 3D vector by a 3x3 matrix is a way of performing three dot products.
Interlude: The Tensor Product and Matrix Representations
The tensor product of two 3D vectors g and e is a 3x3 matrix.
It is easy to remember how to compute it by setting it up as a matrix
product, writing the first vector, g, as a 3x1 matrix and the second vector,
e, as a 1x3 matrix:
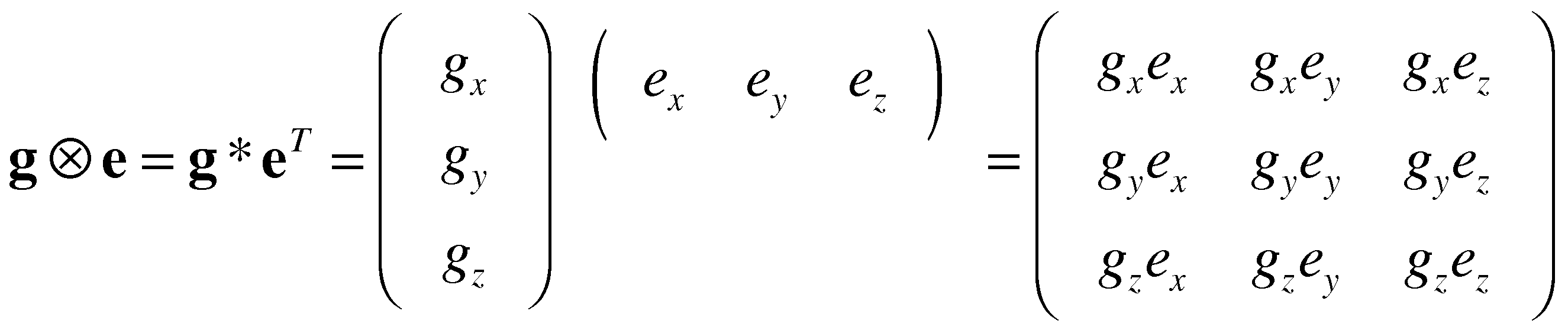
We introduce the tensor product at this juncture because it will help us express as
matrix operations some of the
expressions we have already seen and will continue to see. For example, many vector expressions we will derive include terms like the
(â·b)â we saw in vector decomposition. The general
case is an
expression of the form (e · f)g.
Using the definition of the tensor product above, it is straightforward to verify
(and it is left as an exercise for the reader to do so):
(e · f)g = (g ⊗ e)f = (g ⊗ f)e
This means, for example, we can compute:
We can therefore view (â ⊗ â) as a matrix operator which, when applied to an arbitrary vector, produces the component of that vector
parallel to â. We can compute b⊥ using a similar derivation:
|
b⊥ = b - (â·b)â =
Ib - (â ⊗ â)b = (I - â ⊗ â)b
|
where I is the 3x3 identity matrix.
These observations and formulas will be of great value to us, and you should be sure you
fully understand them!
Cross Product: a×b
The cross product of two 3D vectors is another vector in the same 3D
vector space.
| | Mathematical Definition |
Computational Definitions |
 |
Since the result is a vector, we must specify both the length and the
direction of the resulting vector:
-
length(a × b) = |a × b| =
|a| |b| sinΘ
- direction(a × b) = ⊥ to both a and b
with sense from the right-hand rule
|
Two equally useful characterizations:
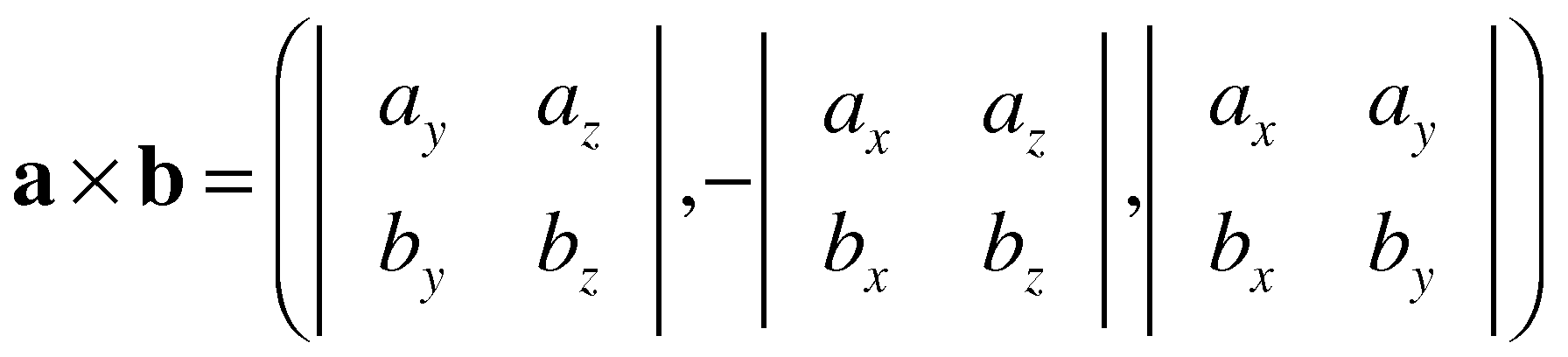
and using the 3x3 "cross product matrix" C(a):
a×b = C(a)b
where:
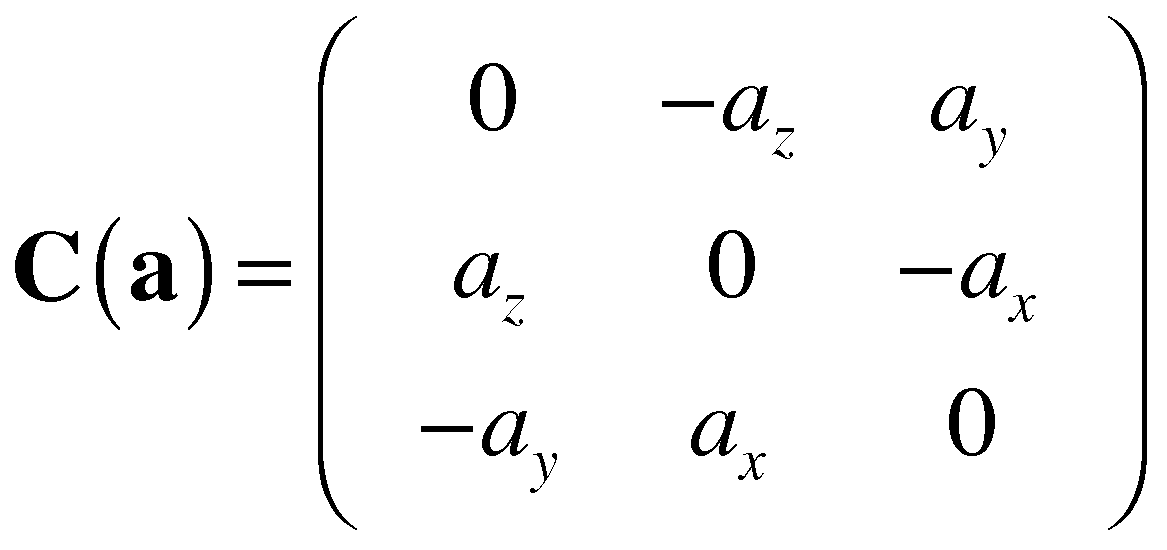
|
Applications
By definition, it computes a vector perpendicular to two given vectors. This is
useful in several contexts, for example:
- Compute a vector perpendicular to a triangle.
- Given two perpendicular vectors, compute a third to complete the definition
of a local coordinate system. (This may follow application of dot product
application #3 above; it will be a part of determining the view orientation
transformation; and it just tends to be useful in a number of contexts.)
- Find a rotation axis that can be used to rotate a vector p onto another
vector q. This operation is useful in many contexts, not the least
important of which is animation.