P
P
u
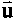
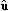
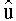
f
f
M
M
| Quantity | In print | Handwritten |
| point in an affine space | upper case italic P |
upper case P |
| 'geometric' vector in a vector space | lower case bold u |
lower case with arrow on top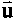 |
| a unit length vector | lower case bold with 'hat'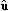 |
lower case with 'hat'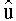 |
| a scalar (i.e., a floating point numeric constant) | lower case italic f |
lower case f |
| a matrix | upper case bold M |
upper case M |
| Operation in print | Underlying coordinate-based interpretation |
| u + v | ( ux+vx , uy+vy , uz+vz ) |
| fu | ( fux , fuy , fuz ) |
| Operation in print | Underlying coordinate-based interpretation |
| P - Q | ( Px-Qx , Py-Qy , Pz-Qz ) |
| P + u | ( Px+ux , Py+uy , Pz+uz ) |
While not directly permitted by the definitions, the validity of the operations shown in the first column of the table below can be immediately established as indicated in the second column.
| Operation in print | Expressed using valid operations | Underlying coordinate-based interpretation |
| u - v | u + (-1)*v | ( ux-vx , uy-vy , uz-vz ) |
| u / f | (1/f) * u | ( ux / f , uy / f , uz / f ) |
| P - u | P + (-1)*u | ( Px-ux , Py-uy , Pz-uz ) |
The following two expressions are algebraically equivalent. Therefore, they would both evaluate to the same triple of numbers, given values for the constituent points and vectors. One of these expressions uses only the operations directly permitted by our vector and affine space definitions. The other does not.
Should we be concerned about this? How should we handle this in general? What are the conditions under which some given expression -- which utilizes undefined operations -- is in fact a sensible, well-defined expression?
(P - Q) + 3(R - X) + 4u
3R - 3X - Q + P + 4u