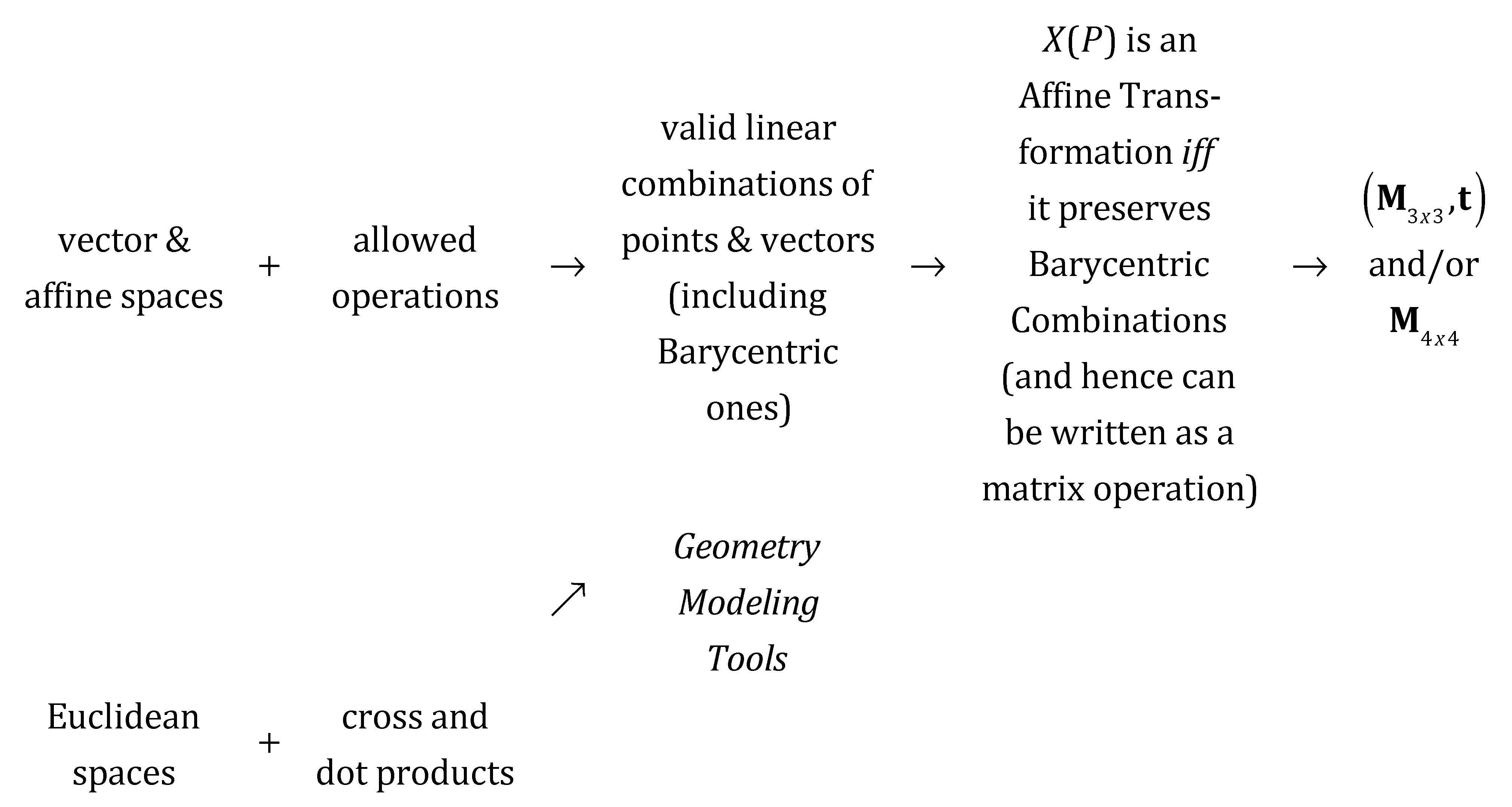
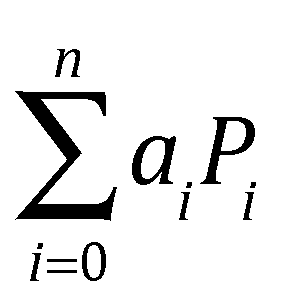 in which
in which
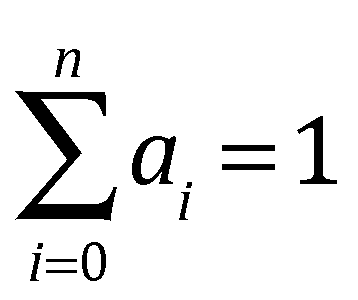 .
.
In addition, if R is defined as the Barycentric combination:
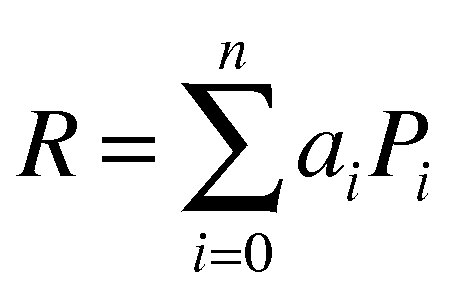
We will write this functionally as:
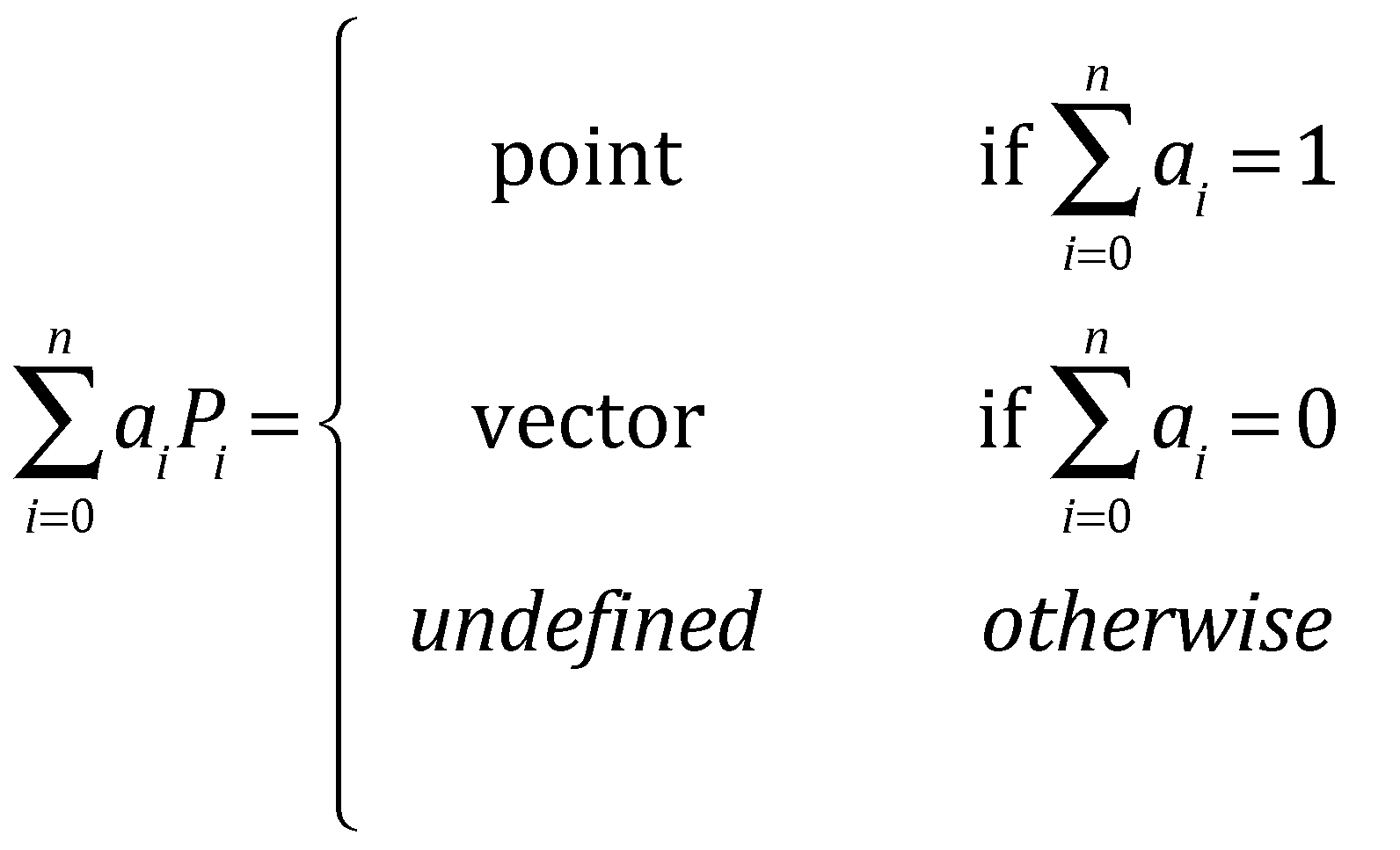
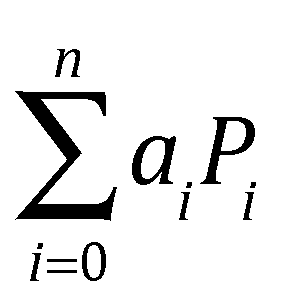 in which
in which
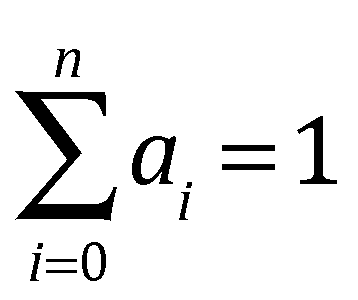 .
.
In addition, if R is defined as the Barycentric combination:
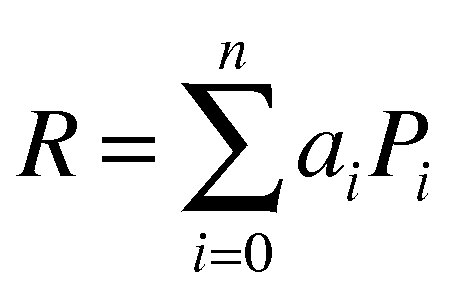
We will write this functionally as:
Given R defined as:
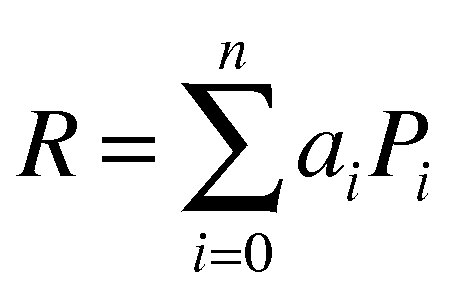
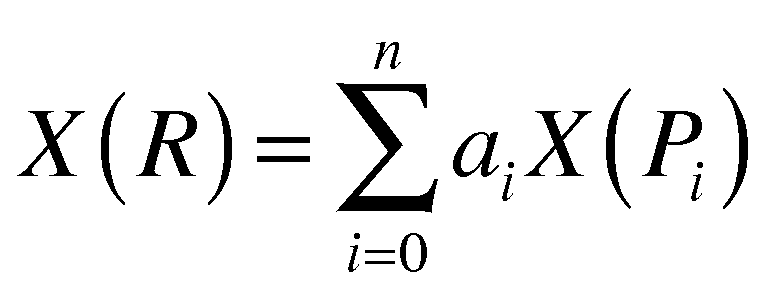
It can be proven that X preserves Barycentric Combinations (and hence is an affine transformation on points in a d-dimensional affine space) if and only if it can be written as:
Creating and rendering 3D models is just a specific case of all this with d=3. In the equation for X(Q) in the previous item, M is a d x d matrix. Our interest is in 3D geometry (i.e., d=3), so let's be explicit and replace M with M3x3. Then we will embed our generic 3D point, Q, on the w=1 plane of projective space so that we can write:

Then X(Q) is just the first three elements of the left-hand side. Moreover, perspective projections (our "exception" from #1) can be represented using a 4x4 matrix with a bottom row different from (0, 0, 0, 1), so we have a representational form that can encode both affine and projective transformations.