Bezier Curve Properties
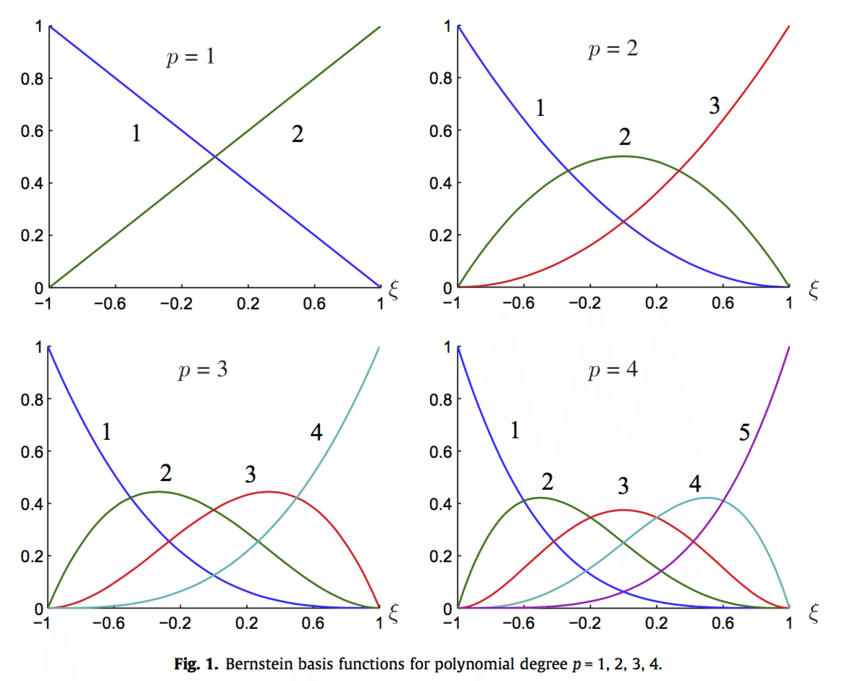
Several important properties of Bezier curves are summarized here. Many of these can
be understood by examining the Bernstein
blending functions used to define Bezier curves.
-
The k-th derivative at the start (end) of a Bezier curve depends only on the
first (last) (k+1) control points. Two obvious special cases:
- k=0:
The Bezier curve starts at the first control point and
stops at the last control point. (In general, it will not pass through any
other control point.)
- k=1:
The vector tangent to the Bezier curve at the start (stop) is
parallel to the line connecting the first two (last two) control
points.
- A Bezier curve will always be completely contained inside of
the Convex Hull of the control points. For planar curves,
imagine that each control point is a nail pounded into a board. The
shape a rubber band would take on when snapped around the control
points is the convex hull. For Bezier curves whose control points
do not all lie in a common plane, imagine the control points are
tiny balls in space, and image the shape a balloon will take on if
it collapses over the balls. This shape is the convex hull in that
case. In any event, a Bezier curve will always lie entirely inside
its planar or volumetric convex hull.
-
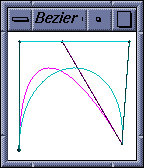 Closely related to the previous is the
fact that adjusting the position of a control point changes the shape of
the curve in a "predictable manner". Intuitively, the curve
"follows" the control point. In the image below, see how a curve defined in
terms of four control points (the magenta curve) changes when one
of its control points is moved to the right, yielding the modified
(cyan) curve.
Closely related to the previous is the
fact that adjusting the position of a control point changes the shape of
the curve in a "predictable manner". Intuitively, the curve
"follows" the control point. In the image below, see how a curve defined in
terms of four control points (the magenta curve) changes when one
of its control points is moved to the right, yielding the modified
(cyan) curve.
- There is no local control of
this shape modification. Every point on the curve (with the
exception of the first and last) move whenever any interior control
point is moved. This property can also be observed in the image
shown in the previous item.
-
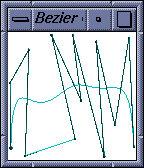 Also related to property #2 is the
fact that Bezier curves exhibit a variation diminishing
property. Informally this means that the Bezier curve will not
"wiggle" any more than the control polygon does. In other words,
the curve will not wiggle unless the designer specifically
introduces wiggling in the control polygon. More formally, the
variation diminishing property can be stated as follows: any
straight line will intersect legs of the control polygon at least
as many times as it crosses the Bezier curve itself. See the
example below which illustrates the property with a degree 12
Bezier curve:
Also related to property #2 is the
fact that Bezier curves exhibit a variation diminishing
property. Informally this means that the Bezier curve will not
"wiggle" any more than the control polygon does. In other words,
the curve will not wiggle unless the designer specifically
introduces wiggling in the control polygon. More formally, the
variation diminishing property can be stated as follows: any
straight line will intersect legs of the control polygon at least
as many times as it crosses the Bezier curve itself. See the
example below which illustrates the property with a degree 12
Bezier curve:
- The effect of control point Pi on
the curve is at
its maximum at parameter value t = i/n. Among other things, this somewhat ameleriorates
problems related to the fact that there is no local control (property #4).
- Bezier curves exhibit a symmetry property: The same
Bezier curve shape is obtained if the control points are specified
in the opposite order. The only difference will be the parametric
direction of the curve. The direction of increasing parameter
reverses when the control points are specified in the reverse
order.
- Bezier curves are invariant under affine transformations, but they are
not invariant under projective transformations.
- Bezier curves are also invariant under affine parameter transformations.
That is, while the curve is usually defined on the parametric interval [0,1],
an affine transformation mapping [0,1] to the interval [a,b], a≠b, yields
the same curve.
 Closely related to the previous is the
fact that adjusting the position of a control point changes the shape of
the curve in a "predictable manner". Intuitively, the curve
"follows" the control point. In the image below, see how a curve defined in
terms of four control points (the magenta curve) changes when one
of its control points is moved to the right, yielding the modified
(cyan) curve.
Closely related to the previous is the
fact that adjusting the position of a control point changes the shape of
the curve in a "predictable manner". Intuitively, the curve
"follows" the control point. In the image below, see how a curve defined in
terms of four control points (the magenta curve) changes when one
of its control points is moved to the right, yielding the modified
(cyan) curve.
 Also related to property #2 is the
fact that Bezier curves exhibit a variation diminishing
property. Informally this means that the Bezier curve will not
"wiggle" any more than the control polygon does. In other words,
the curve will not wiggle unless the designer specifically
introduces wiggling in the control polygon. More formally, the
variation diminishing property can be stated as follows: any
straight line will intersect legs of the control polygon at least
as many times as it crosses the Bezier curve itself. See the
example below which illustrates the property with a degree 12
Bezier curve:
Also related to property #2 is the
fact that Bezier curves exhibit a variation diminishing
property. Informally this means that the Bezier curve will not
"wiggle" any more than the control polygon does. In other words,
the curve will not wiggle unless the designer specifically
introduces wiggling in the control polygon. More formally, the
variation diminishing property can be stated as follows: any
straight line will intersect legs of the control polygon at least
as many times as it crosses the Bezier curve itself. See the
example below which illustrates the property with a degree 12
Bezier curve:
