Due: 2 March 2020 (emailed by 11:59:59 p.m.)

This project is motivated by exercise #5 on page 160 of the textbook. The following provides explicit specifications for this project and gives a few starting hints for how to attack the design and implementation.

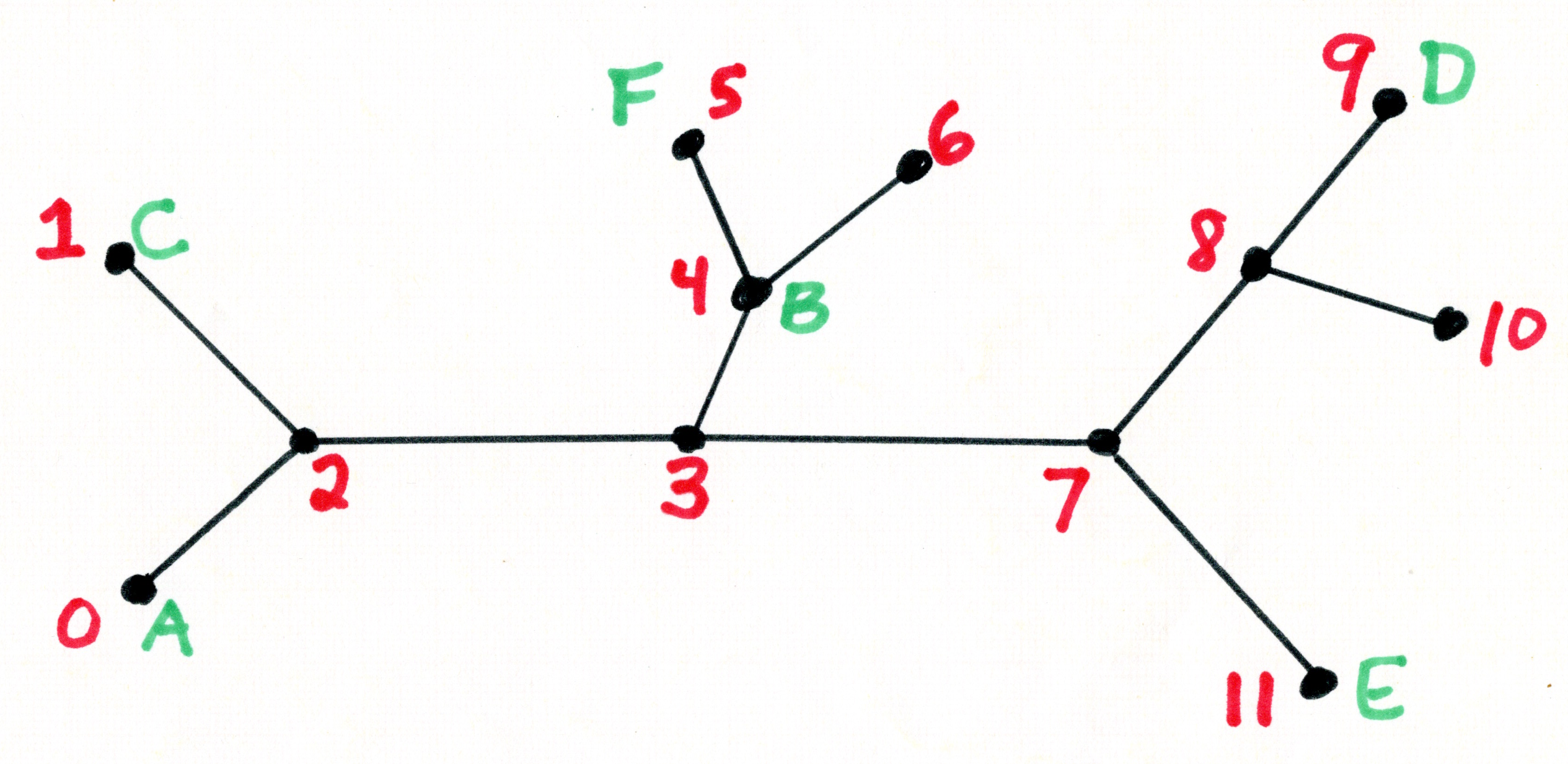
Stations are numbered starting from 0; trains are identified by a letter starting with 'A'. At the start of a given day, the trains are at the indicated stations. The routes assigned to trains for the day are: A: 0 2 3 4 6 4 3 7 11 B: 4 3 7 8 9 C: 1 2 3 7 11 7 8 D: 9 8 7 3 2 1 E: 11 7 3 4 5 F: 5 4 3 2 0

1. Get the name of an input file from argv[1]. This file will describe the number of trains and stations as well as the routes of each train. Its general format will be:

   nTrains  nStations
   num-stations-in-train-0-route  station-0 station-1 …
   …ditto for all the rest of the trains…

   Here is the input file that describes the routes depicted in the figure on the right. Assume that each train is at the first station in its route at the start of the day.

   Note that stations are numbered 0..nStations-1. The diagram on the right is simply to help you visualize the task. You should not create any explicit model of how (or if) stations are connected by tracks. Doing so makes this problem considerably harder than it needs to be. You are simply to assume that if station i immediately precedes station j in the route for some train that there is a track of unit length that connects the two stations. All trains travel at unit speed, so in one time step, any train can get from one station to another.

2. When your program starts, read the file, launch one thread for each train, passing to the thread the route it is to follow. Make sure no thread actually starts processing its route until all n threads have been created and launched. You can use the "bool go" scheme for this, but use the "std::atomic_int active(0);" control as well.
3. Once started, your threads must log train progress as indicated in this sample output. (Note that each run will typically produce a different sequence, but each sequence must be valid, and the reported time steps must be monotonically increasing. In addition, be sure to identify trains by letter and stations by number as shown in the sample output.) Each train thread must log its own progress. So, for example, do not assign all writing to output to a single thread. Be sure to use std::mutex to keep the output from being garbled due to several threads trying to write at the same time.
4. Make sure the critical sections of your code are no longer than they absolutely need to be. For example, do not lock down large chunks of the body of your train loop just to simplify your coding!

Project Development & Hints

Create a directory (say, "project1") for your code and place your source code and any data files you use in this directory. Here is a sample Makefile that assumes a one-file submission. If you use multiple source files (e.g., class headers and implementation files), then just update the dependency lists and add compilation directives as usual.

The simulation is to proceed one time step at a time. Each thread will loop through its assigned route. Each trip through the loop simulates one time step. On each step, a train will either successfully acquire its track and move to the next station, or it will be forced to stay at its current station until the next time step. After each time step, each train thread that has not finished its route must report its progress (or lack thereof) as indicated in the sample report. You will need to use a barrier at the end of each time step to keep a train from moving on before all other trains have finished their processing for the time step. You can use the Barrier class on the web site: Barrier.h.

Each station can hold an arbitrary number of trains, but only one train at a time can be on any track. So, for example, if train Q is traveling from station 5 to station 4 in some time step, no other train can be on that track traveling in either direction! Therefore, the critical resource to be managed is the single track between stations. The obvious approach is to use mutex instances to control access to tracks.

Grading Criteria

Note that I will run your projects using one or more data sets other than the one given here, so be sure your implementation is general and makes no unnecessary assumptions about the input data set. In addition, I will run your program many times with each data set (just as I have shown you in class) to see if it ever hangs or otherwise produces invalid output. If I see any such problems – even if you never saw them – your submission will be considered to have a bug. To be fair, I will only enforce this when running on the department linux machines (cycle servers or machines in the fishbowl and B-D rooms). I strongly encourage you to try your projects on as many different machines as you reasonably can.

Specific criteria:

1. (45/100): Correctness
   • Always produces valid (but not identical) results for all valid input files and across multiple executions. (In fact, consistently producing identical results is typically an indication that some design criterion specified above has been violated. One common example: making a critical section larger than needed.)
   • Assigned train responsibilities properly performed.
2. (25/100): Proper use of C++ threading tools (including synchronization that minimizes sizes of critical sections of code)
3. (25/100): Correct output from each of the n threads, reported in proper chronological order and with correct labels for trains and stations.
4. (5/100): Adherence to all other specific criteria given in the assignment (e.g., get file from argv[1], synchronized start of all threads)

If your submission ever hangs or aborts, points will be deducted from the total you have otherwise earned.

Project Submission

Remove object files (e.g., main.o), if any, and your linked executable program (e.g., main), keeping any data files you have created in the directory. Then create and send a tar file of the project1 directory to me at jrmiller@ku.edu.