Comparing Planar Geometric Projections

Preliminaries

A 3D to 2D projection can be characterized by specifying (i) a "family of projection lines", and (ii) a projection plane. Each line in the family must intersect the projection plane in exactly one point.

For any given 3D point, Q (with the possible exception of one), there must be exactly one projection line in the family passing through Q. The 2D projection of the 3D point Q is the point Q′ on the projection plane at which the corresponding line intersects it.

Even though the immediate goal is to determine how our 3D geometry will project and appear on our 2D display, we will want the matrix representation to encode a "3D to 3D projection". Specifically, we will want to preserve a measure of depth so that subsequent graphics pipeline processes such as visible surface determination will be able to function correctly.

The Three Most Common Planar Geometric Projections

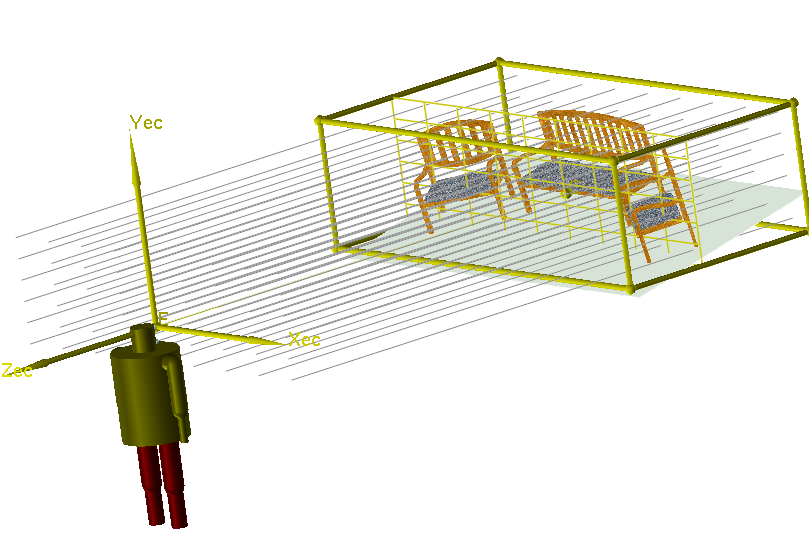
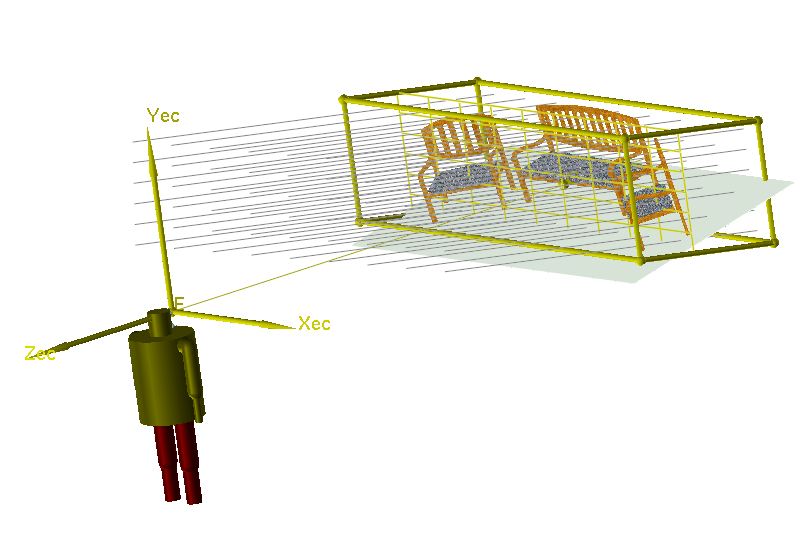
Each of the images in the first column below was generated using the same model coordinate to eye coordinate transformation (i.e., the same (eye, center, up) specification), but with the different projections illustrated in the second column.

⇒ Note, too, that the Model Coordinate axes are not shown here. That coordinate system is no longer relevant in the context of projections!

Relevant Class Method Declarations in Matrix4x4.h

static Matrix4x4 perspective(double ecZpp, double ecXmin, double ecXmax, double ecYmin, double ecYmax, double ecZmin, double ecZmax);

static Matrix4x4 orthogonal (              double ecXmin, double ecXmax, double ecYmin, double ecYmax, double ecZmin, double ecZmax);

static Matrix4x4 oblique    (double ecZpp, double ecXmin, double ecXmax, double ecYmin, double ecYmax, double ecZmin, double ecZmax, const AffVector& ecProjDir);

In the drawings below, the yellow view volume depicts the region of space which will be visible; its shape and extent are defined by the projection type along with the specific (ecXmin, ecXmax, ecYmin, ecYmax, ecZmin, ecZmax) values. The xy-portion of this view volume is defined to be on the projection plane, depicted in the drawings as the grid perpendicular to the line of sight (and hence parallel to the ecZmin and ecZmax planes).

A Historical Reference

My favorite classical reference for understanding planar geometric projections, including history, classification, current usage, and mathematics is:

• Planar Geometric Projections and Viewing Transformations, Ingrid Carlbom and Joseph Paciorek, ACM Computing Surveys, Vol. 10, No. 4, December 1978, pages 465-502.

Examples

Example 1: Teapot and XYZ Cube

	Image Generated	The metaview
Perspective Family characterized as all lines passing through a common point
Orthogonal One type of parallel projection in which all family lines are perpendicular to the projection plane
Oblique One type of parallel projection in which all family lines meet the projection plane at some angle other than 90 degrees

Example 2: Chair Garden

	Image Generated	The metaview
Perspective Family characterized as all lines passing through a common point
Orthogonal One type of parallel projection in which all family lines are perpendicular to the projection plane
Oblique One type of parallel projection in which all family lines meet the projection plane at some angle other than 90 degrees